
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点P2018的坐标为( )
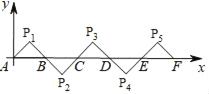
A. (4030,1) B. (4029,﹣1)
C. (4033,1) D. (4035,﹣1)
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
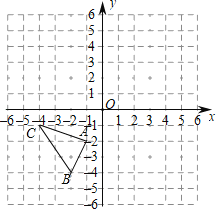
【题目】如图,平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)在平面直角坐标系中画出与△ABC关于点P(1,0)成中心对称的△A'B'C',并分别写出点A',B',C'的坐标;
(2)如果点M(a,b)是△ABC边上(不与A,B,C重合)任意一点,请写出在△A'B'C'上与点M对应的点M'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
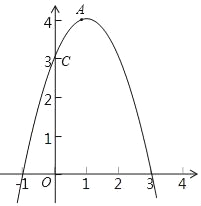
【题目】如图,已知二次函数y=ax2+2x+c图象经过点A (1,4)和点C (0,3).
(1)求该二次函数的解析式;
(2)结合函数图象,直接回答下列问题:
①当﹣1<x<2时,求函数y的取值范围: .
②当y≥3时,求x的取值范围: .
查看答案和解析>>
科目:初中数学 来源: 题型:
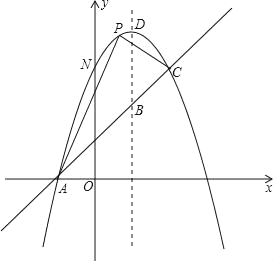
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0)、C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)设点M(3,n),求使MN+MD取最小值时n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于代数式,不同的表达形式能表现出它的不同性质.例如代数式![]() ,若将其写成
,若将其写成![]() 的形式,就能看出不论字母x取何值,它都表示正数;若将它写成
的形式,就能看出不论字母x取何值,它都表示正数;若将它写成![]() 的形式,就能与代数式B=
的形式,就能与代数式B=![]() 建立联系.下面我们改变x的值,研究一下A,B两个代数式取值的规律:
建立联系.下面我们改变x的值,研究一下A,B两个代数式取值的规律:
x | -2 | -1 | 0 | 1 | 2 | 3 |
| 10 | 5 | 2 | 1 | 5 | |
| 17 | 10 | 5 |
(1)完成上表;
(2)观察表格可以发现:
若x=m时,![]() ,则x=m+1时,
,则x=m+1时,![]() .我们把这种现象称为代数式A参照代数式B取值延后,此时延后值为1.
.我们把这种现象称为代数式A参照代数式B取值延后,此时延后值为1.
①若代数式D参照代数式B取值延后,相应的延后值为2,求代数式D;
②已知代数式![]() 参照代数式
参照代数式![]() 取值延后,请直接写出b-c的值:________.
取值延后,请直接写出b-c的值:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com