
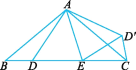
【题目】已知AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD',连接D'E.

(1)如图①,当∠BAC=120°,∠DAE=60°时,求证DE=D'E.
(2)如图②,当DE=D'E时,∠DAE与∠BAC有怎样的数量关系?请写出,并说明理由.
【答案】(1)详见解析;(2)∠DAE=![]() ∠BAC,理由详见解析.
∠BAC,理由详见解析.
【解析】
(1)根据旋转的性质和全等三角形的判定定理SAS证得△DAE≌△D′AE,则由“全等三角形的对应边相等”的性质证得结论;
(2)∠DAE=![]() ∠BAC.根据旋转的性质和全等三角形的判定定理SSS证得△DAE≌△D′AE,则由“全等三角形的对应角相等”的性质推知∠DAE=
∠BAC.根据旋转的性质和全等三角形的判定定理SSS证得△DAE≌△D′AE,则由“全等三角形的对应角相等”的性质推知∠DAE=![]() ∠BAC.
∠BAC.
(1)证明:如图,

∵△ABD旋转得到△ACD',
∴∠DAD'=∠BAC=120°,AD=AD'.
∵∠DAE=60°,
∴∠EAD'=∠DAD'-∠DAE=120°-60°=60°.
∴∠DAE=∠D'AE,
又∵AE=AE,AD=AD',
∴△DAE≌△D'AE(SAS).
∴DE=D'E.
(2)解:∠DAE=![]() ∠BAC.
∠BAC.
理由:如图,
∵△ABD旋转得到△ACD',
∴∠DAD'=∠BAC,AD=AD'.
∵DE=D'E,AE=AE,
∴△DAE≌△D'AE(SSS).
∴∠DAE=D'AE=![]() ∠DAD'.
∠DAD'.
∴∠DAE=![]() ∠BAC.
∠BAC.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
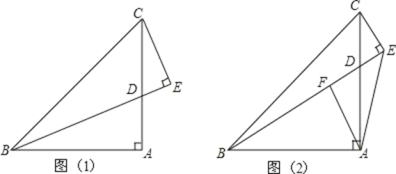
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() =
=![]() 的图像与正比例函数
的图像与正比例函数![]() =
=![]() 的图像相交于点A(2,
的图像相交于点A(2,![]() ),与
),与![]() 轴相交于点B.
轴相交于点B.

(1)求![]() 、
、![]() 的值;
的值;
(2)在![]() 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |

(1)求A的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com