
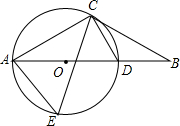
 如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.
如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.分析 (1)连接OC,根据CD⊥AC得出AD是⊙O的直径再由等腰三角形的性质得出∠OAC=∠OCA=30°,故∠COB=60°.根据三角形内角和定理得出∠OCB=90°,由此可得出结论;
(2)连接DE,由角平分线的性质得出∠ACE=∠DCE,故可得出$\widehat{AE}$=$\widehat{DE}$,AE=DE,再由勾股定理即可得出结论.
解答 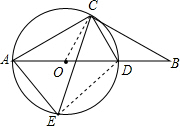 (1)证明:连接OC,
(1)证明:连接OC,
∵CD⊥AC,
∴AD是⊙O的直径.
∵OA=OC,
∴∠OAC=∠OCA=30°,
∴∠COB=60°.
∵AC=BC,∠CAB=30°,
∴∠B=30°,
∴∠OCB=90°,
∴BC是⊙O的切线;
(2)解:连接DE,
在Rt△ACD中,
∵∠CAD=30°,CD=1,
∴AD=2CD=2,
∵CE平分∠ACD交⊙O于点E,
∴∠ACE=∠DCE,
∴$\widehat{AE}$=$\widehat{DE}$,
∴AE=DE.
设AE=x,由勾股定理得,x2+x2=22,解得x=$\sqrt{2}$,即AE=$\sqrt{2}$.
点评 本题考查的是切线的性质,根据题意作出辅助线,构造出直角三角形,利用三角形内角和定理及勾股定理求解是解答此题的关键.


科目:初中数学 来源: 题型:解答题
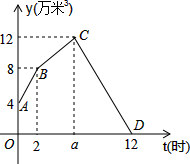 某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.若这3个水口的水流都是匀速的,水池中的蓄水量y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题:
某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.若这3个水口的水流都是匀速的,水池中的蓄水量y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
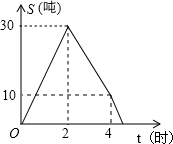 某储运部紧急调拨一批物资,连续4小时调进物资,当开始调进物资2小时后又同时开始调出物资,储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,下列说法:
某储运部紧急调拨一批物资,连续4小时调进物资,当开始调进物资2小时后又同时开始调出物资,储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,下列说法:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
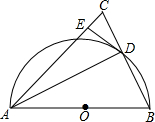 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
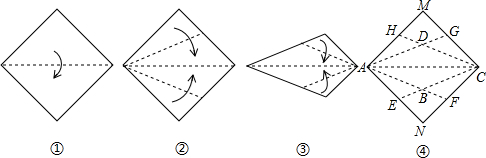 在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开.
在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 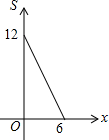 | B. | 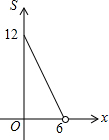 | C. | 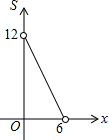 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=4,ED=8.
如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=4,ED=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三内角之比为1:2:3 | B. | 三边长的平方之比为1:2:3 | ||
| C. | 三边长之比为3:4:5 | D. | 三内角之比为3:4:5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com