|
|
|
在平面直角坐标系中,已知点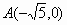 , ,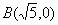 ,点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C的坐标________. ,点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C的坐标________.
|
|
|
答案:
解析:
|
(0,2),(0,-2),(-3,0),(3,0).
解析:①当点C位于y轴上时,设C(0,b).则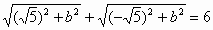 ,解得b=2或b=-2,此时C点坐标为(0,2)或(0,-2). ,解得b=2或b=-2,此时C点坐标为(0,2)或(0,-2).
②当点C位于x轴上时,设C(a,0).
则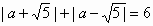 ,即2a=6或-2a=6, ,即2a=6或-2a=6,
解得a=3或a=-3,
此时C点坐标为(-3,0)或(3,0).
综上所述,点C的坐标是(0,2),(0,-2),(-3,0),(3,0).
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
若直角三角形的两直角边长分别为a、b,且满足 ,则该直角三角形的斜边长为________. ,则该直角三角形的斜边长为________.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
将直角三角形三边扩大同样的倍数,得到的三角形是
|
| [ ] |
A. |
锐角三角形
|
B. |
直角三角形
|
C. |
钝角三角形
|
D. |
任意三角形
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:阅读理解
|
|
|
阅读下列解题过程:
已知a、b、c为△ABC的三边,且满足a2c2-b2c2=a4b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4, ①
∴c2(a2-b2)=(a2+b2)(a2-b2). ②
∴c2=a2+b2. ③
∴△ABC是直角三角形. ④
(1)上述解题过程是从哪一步开始出错的?写出代号,并注明原因.
(2)写出本题的正确结论,并写出推导过程.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
已知Rt△ABC中,∠C=90°,若a+b=14 cm,c=10 cm,则Rt△ABC的面积是
|
| [ ] |
A. |
24 cm2
|
B. |
36 cm2
|
C. |
48 cm2
|
D. |
60 cm2
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在水塔O的东北方向32 m处有一抽水站A,在水塔的东南方向24 m处有一建筑工地B,在A、B间建一条直水管,则水管的长为
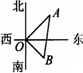
|
| [ ] |
A. |
45 m
|
B. |
40 m
|
C. |
50 m
|
D. |
56 m
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,南北向MN为我国的领海线,即MN以西为我国领海,以东为公海.上午9时50分,我国反走私艇A发现正东方有一走私艇C以每小时13海里的速度偷偷向我领海开来,便立即通知正在线上巡逻的我国反走私艇B密切注意.反走私艇A通知反走私艇B:A和C两艇的距离是13海里,A、B两艇的距离是5海里.反走私艇B测得距离C艇是12海里,若走私艇C的速度不变,最早会在什么时间进入我国领海?
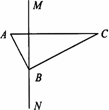
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在菱形ABCD中,E,F、G、H分别是菱形四边的中点,连接EG与FH交于点O,则图中共有菱形
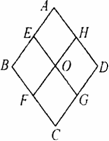
|
| [ ] |
A. |
4个
|
B. |
5个
|
C. |
6个
|
D. |
7个
|
|
|
查看答案和解析>>

 阅读快车系列答案
阅读快车系列答案