

���� ��1����AB���е�O����ͨ��ͬԲ�İ뾶��ȣ�ȡOC=AB�����ABC���������������������Σ�
��2����ͼ2���������ߣ������ȱ������Σ�֤����CDE�ǵȱ������Σ��á�DCE=��DEC=60�㣬���ԡ�ECB=30����EF=x���ֱ��ʾBC=2$\sqrt{3}$x��AC=2DC=2CE=4x���������ֵ���ɣ�
��3������ͼ3������APQΪ���������Σ���ʱPQ=AE����Ϊ��P��Qͬʱ�ӵ�A������������ͬ���ٶ��˶�������AB+BP=AD+DQ����BP=DQ�����ݵ�ʽ�����ʺ������εı߳���ȵã�PC=CQ����֤����ABP�ա�ADQ����AP=AQ���ɵ������������ߺ�һ�����ʵã�AE��PQ����PAE=��QAE����֤��AE��AC���ߣ�
��CE=x����ʾPQ=AE=2x�����ݹ��ɶ����з������x��ֵ�����������ʽ�������ε�������ɣ�
����ͼ4����AP=EQʱ���������ߣ���AG=x����AP=AQ=4x���ȱ�ʾAP���QG�ij������������ʽ�ɼ�������
��� 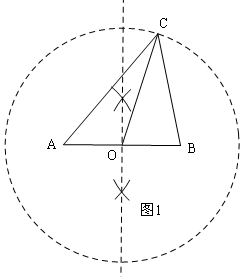 �⣺��1������������AB���д��ߣ���AB��O��
�⣺��1������������AB���д��ߣ���AB��O��
����OΪԲ�ģ���ABΪ�뾶��Բ����Բ������ȡһ��C��
������AC��BC��
���ABC����������������������
��2����ͼ2��ȡBD���е�E������CE����E��EF��BC��F��
�ߡ�C=90�㣬
��CE=$\frac{1}{2}$BD=BE��
��D��AC���е㣬E��BD���е㣬
��CD=$\frac{1}{2}$AC��DE=$\frac{1}{2}$BD��
��AC=BD��
��CD=DE=CE��
���CDE�ǵȱ������Σ�
���DCE=��DEC=60�㣬
���ECB=90��-60��=30�㣬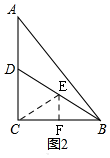
��EF=x����EC=BE=2x��CF=$\sqrt{3}$x��
ͬ��BF=$\sqrt{3}$x��
��BC=2$\sqrt{3}$x��AC=2DC=2CE=4x��
��$\frac{BC}{AC}=\frac{2\sqrt{3}x}{4x}$=$\frac{\sqrt{3}}{2}$��
��3�������������
����ͼ3������APQΪ���������Σ���ʱPQ=AE��
������ã�AB+BP=AD+DQ��
���ı���ABCDΪ�����Σ�
��AB=AD=BC=CD��
��BP=DQ��
��BC-BP=CD-DQ��
��PC=CQ��
�ߡ�B=��D=90�㣬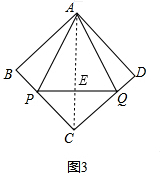
���ABP�ա�ADQ��
��AP=AQ��
��AEΪ���ߣ�
��AE��PQ����PAE=��QAE��
����AC��
��AP=AQ��PC=CQ��
��ACΪPQ���д��ߣ�
��AE��AC���ߣ�
���ı���ABCDΪ�����Σ�
���BCD=90�㣬
��E��PQ���е㣬
��CE=$\frac{1}{2}$PQ=PE=EQ��
��CE=x����PE=EQ=x��PQ=AE=2x��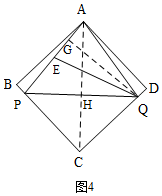
Rt��ABC��AB=6��
��62+62=AC2=��AE+CE��2��
72=��2x+x��2��
x=$��2\sqrt{2}$��
��x��0��
��PQ=AE=2x=4$\sqrt{2}$��
��S��APQ=$\frac{1}{2}$PQ•AE=$\frac{1}{2}$��4$\sqrt{2}$��4$\sqrt{2}$=16��
����ͼ4������APQΪ���������Σ���ʱAP=EQ��
��E��QG��AP��G��
��AP=AQ=EQ��
��AG=EG��
��AE=EP��
��AG=x����AP=AQ=4x��
��QG=$\sqrt{A{Q}^{2}-A{G}^{2}}$=$\sqrt{��4x��^{2}-{x}^{2}}$=$\sqrt{15}$x��
����AC��PQ��H����AC��PQ��
��CH=a����QH=a��AH=6$\sqrt{2}$-a��
Rt��AHQ��AQ2=AH2+HQ2��
��$��4x��^{2}=��6\sqrt{2}-a��^{2}+{a}^{2}$��
16x2=72-12$\sqrt{2}$a+2a2 �٣�
S��APQ=$\frac{1}{2}$AP•QG=$\frac{1}{2}$PQ•AH��
4x$•\sqrt{15}$x=2a��6$\sqrt{2}$-a����
$4\sqrt{15}{x}^{2}$=12$\sqrt{2}$a-2a2 �ڣ�
�ɢٺ͢ڵã�16x2=72-4$\sqrt{15}$x2��
��16+4$\sqrt{15}$��x2=72��
x2=18��4-$\sqrt{15}$����
��S��APQ=$\frac{1}{2}$AP•QG=$\frac{1}{2}$•4x$•\sqrt{15}$x=2$\sqrt{15}$��18��4-$\sqrt{15}$��=144$\sqrt{15}$-540��
��������������APQ�ǡ����������Ρ�ʱ����APQ�������16��144$\sqrt{15}$-540��
���� �������ı��ε��ۺ��⣬�����������ε����ʡ�ֱ��������б�����ߵ����ʣ����������ε������Լ�������ȫ�ȵ����ʺ��ж�������һ���¶�����Ķ��������⼰�߹���ͼ�⣬�ۺ��Խ�ǿ�������������ʺͶ����ǹؼ�����ע�������������֪�ġ����߳�ǡ�õ�����ߵij�����һ������


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
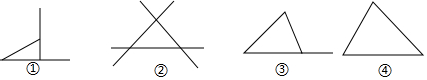
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�������߶�������Ϊ��C��2��8������x���ڵ�A��6��0������y���ڵ�B��
��ͼ�������߶�������Ϊ��C��2��8������x���ڵ�A��6��0������y���ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�BDƽ�֡�ABC��BC���д��߽�BC�ڵ�E����BD�ڵ�F������CF��
��ͼ����ABC�У�BDƽ�֡�ABC��BC���д��߽�BC�ڵ�E����BD�ڵ�F������CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣮
��ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����Rt��ABC�У���BAC=90�㣬AD��BC�ڵ�D�������н��۲���ȷ���ǣ�������
��ͼ����Rt��ABC�У���BAC=90�㣬AD��BC�ڵ�D�������н��۲���ȷ���ǣ�������| A�� | cosC=$\frac{CD}{AC}$ | B�� | cosC=$\frac{AC}{BC}$ | C�� | cosC=$\frac{AD}{AC}$ | D�� | cosC=$\frac{AD}{AB}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A��-5��0�����Գ���Ϊֱ��x=-2�������ĸ����ۣ�
��ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A��-5��0�����Գ���Ϊֱ��x=-2�������ĸ����ۣ�| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
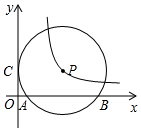 ��ͼ����P��y�������ڵ�C��0��3������x���ཻ�ڵ�A��1��0����B��9��0����˫����y=$\frac{k}{x}$ǡ�þ���Բ��P����ôk��ֵ��15��
��ͼ����P��y�������ڵ�C��0��3������x���ཻ�ڵ�A��1��0����B��9��0����˫����y=$\frac{k}{x}$ǡ�þ���Բ��P����ôk��ֵ��15���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���ABC����������ֱ�ΪA��2��3����B��3��1����C��-2��-2����
��ͼ����ƽ��ֱ������ϵ�У���ABC����������ֱ�ΪA��2��3����B��3��1����C��-2��-2�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com