
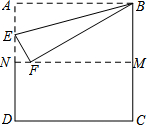
 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,求FM的长.
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,求FM的长.  名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
| 人数 | 平均分 | |
| 甲组 | 100 | 94 |
| 乙组 | 80 | 90 |
| 分数段 | 频数 | 等级 |
| 0≤x<60 | 3 | C |
| 60≤x<72 | 6 | |
| 72≤x<84 | 36 | B |
| 84≤x<96 | ||
| 96≤x<108 | 50 | A |
| 108≤x<120 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
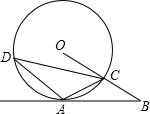 已知,如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=$\frac{1}{2}$OB.
已知,如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=$\frac{1}{2}$OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com