
在平面直角坐标系xoy中,等腰三角形ABC的三个顶点A(0,1),点B在x轴的正半轴上,∠ABO=30°,点C在y轴上.
(1)直接写出点C的坐标为 ;
(2)点P关于直线AB的对称点P′在x轴上,AP=1,在图中标出点P的位置并说明理由;
(3)在(2)的条件下,在y轴上找到一点M,使PM+BM的值最小,则这个最小值为 .
(1) (0,3)或(0,-1);(2)理由见解析;(3)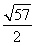 .
.
【解析】
试题分析:(1)先确定A的位置,再作出△AOB,就可以求出AB=2,OB=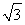 ,在y轴上符合条件的有两点C1和C2,求出即可;
,在y轴上符合条件的有两点C1和C2,求出即可;
(2)根据AP=AO=1,得出P的对称点是O点,求出OC,即可得出OP,解直角三角形求出PQ和OQ即可;
(3)作出B关于y轴的对称点,连接PB′即可得出M点的位置,求出PB′长即可.
试题解析: (1)符合条件的有两点,以A为圆心,以AB为半径画弧,交y轴于C1、C2点,
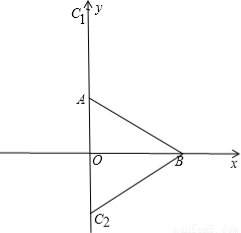
∵A(0,1),
∴OA=1,
∵在Rt△AOB中,OA=1,∠ABO=30°,
∴AB=2OA=2,OB=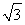 ,
,
即AC1=AC2=2,
∴OC1=1+2=3,OC2=2-1=2,
∴C的坐标是(0,3)或(0,-1),
(2)P的坐标是(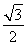 ,
,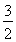 ),
),
理由是:过P作PQ⊥x轴于Q,
∵OA=1,AP=1,AO⊥x轴,
∴x轴和以A为圆心,以1为半径的圆相切,
∵AP=1,
∴P在圆上,
∵点P关于直线AB的对称点P′在x轴上,AP=1,
∴P′点和O重合,如图:
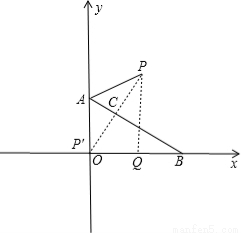
∵P和P′关于直线AB对称,
∴PP′⊥AB,PC=P′C,
由三角形面积公式得:S△AOB=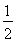 AO×OB=
AO×OB=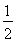 AB×CO,
AB×CO,
∴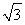 ×1=2OC,
×1=2OC,
∴OC=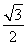 ,
,
∴PP′=2OC=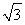 ,
,
∵∠ABO=30°,∠OCB=90°,
∴∠POB=60°,
∴PQ=OP×sin60°=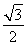 ,OQ=OP×cos60°=
,OQ=OP×cos60°=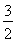 ,
,
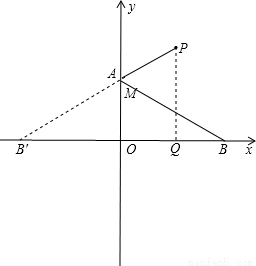
即P的坐标是(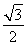 ,
,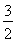 );
);
(3)作B关于y轴的对称点B′,连接PB′交y轴于M,则M为所求,
∵OB=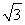 ,
,
∴OB′=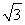 ,
,
即BB′=2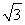 ,
,
∵PQ=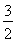 ,
,
∴由勾股定理得:PB′=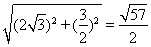 ,
,
∴PM+BM=PM+B′M=PB′=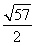 .
.
考点: 1.轴对称-最短路线问题;2.坐标与图形性质;3.等腰三角形的性质.


科目:初中数学 来源:2014年初中数学北师大版七年级上期中检测练习卷(解析版) 题型:选择题
如果a与b互为相反数,则下列各式不正确的是( )
A.a+b=0 B.|a|=|b| C.a-b=0 D.a=-b
查看答案和解析>>
科目:初中数学 来源:2015届山东枣庄永安乡龙子心中学八年级上期末数学试卷(解析版) 题型:选择题
如图,AB∥CD,∠A+∠E=75°,则∠C为( )
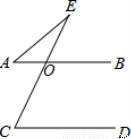
A、60° B、65° C、75° D、80°
查看答案和解析>>
科目:初中数学 来源:2015届北京市朝阳区八年级第一学期期末检测数学试卷(解析版) 题型:填空题
如图,AC=AD,∠1=∠2,只添加一个条件使△ABC≌△AED,你添加的条件是 .

查看答案和解析>>
科目:初中数学 来源:2015届初中数学苏教版八年级上册第六章练习卷(解析版) 题型:填空题
某超市招聘收银员一名,对三名应聘者进行了三项素质测试.下面是三名应聘者的素质测试成绩:
素质测试 | 测试成绩 | ||
小李 | 小张 | 小赵 | |
计 算 机 | 70 | 90 | 65 |
商品知识 | 50 | 75 | 55 |
语 言 | 80 | 35 | 80 |
公司根据实际需要, 对计算机、商品知识、语言三项测试成绩分别赋予权重4、3、2,则这三人中 将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com