
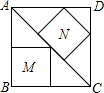
 把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是
把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,小明把一张边长为10厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子,
如图,小明把一张边长为10厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•香坊区一模)如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2.
(2013•香坊区一模)如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2.| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
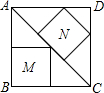 把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是________平方厘米.
把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图所示剪下两个内接正方形M、N,则M、N的面积的差是________平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
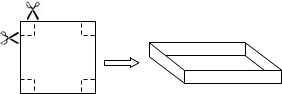 如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2.
如图,在一个边长为40厘米的正方形硬纸板的四角各剪一个边长为xcm的小正方形,将剩余部分折成一个无盖的长方体盒子(纸板的厚度忽略不计),设折成的长方体盒子的侧面积为Scm2. 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值 】
】查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com