
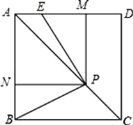
【题目】如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN;
(3)若点P在线段AC上移动,其他不变,设PC=x,AE=y,求y关于x的解析式.
【答案】(1)见解析;(2)见解析;(3) y=﹣![]() x+1.
x+1.
【解析】
(1)由四边形ABCD是正方形,易得∠BAD=90°,AC平分∠BAD,又由PM⊥AD,PN⊥AB,即可证得四边形PMAN是正方形;
(2)由四边形PMAN是正方形,易证得△EPM≌△BPN,即可证得:EM=BN;
(3)首先过P作PF⊥BC于F,易得△PCF是等腰直角三角形,继而证得△APM是等腰直角三角形,可得AP=![]() AM=
AM=![]() (AE+EM),即可得方程
(AE+EM),即可得方程![]() ﹣x=
﹣x=![]() (y+
(y+![]() x),继而求得答案.
x),继而求得答案.
(1)∵四边形ABCD是正方形,
∴AC平分∠BAD,
∵PM⊥AD,PN⊥AB,
∴PM=PN,
又∵∠BAD=90°,∠PMA=∠PNA=90°,
∴四边形PMAN是矩形,
∴四边形PMAN是正方形;
(2)∵四边形PMAN是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE=∠NPB,
在△EPM和△BPN中,
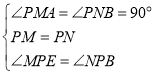 ,
,
∴△EPM≌△BPN(ASA),
∴EM=BN;
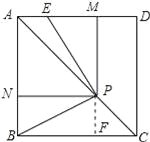
(3)过P作PF⊥BC于F,如图所示:
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=1,∠PCF=45°,
∴AC=![]() =
=![]() ,△PCF是等腰直角三角形,
,△PCF是等腰直角三角形,
∴AP=AC﹣PC=![]() ﹣x,BN=PF=
﹣x,BN=PF=![]() x,
x,
∴EM=BN=![]() x,
x,
∵∠PAM=45°,∠PMA=90°,
∴△APM是等腰直角三角形,
∴AP=![]() AM=
AM=![]() (AE+EM),
(AE+EM),
即![]() ﹣x=
﹣x=![]() (y+
(y+![]() x),
x),
解得:y=﹣![]() x+1.
x+1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵![]() ,即
,即![]() ,
,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() -2).
-2).
请解答:(1) ![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知: 10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的甲型号手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)一月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型号每台进价为3500元,乙型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
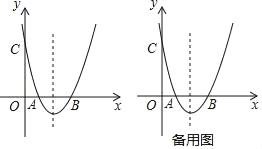
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线y=x2+bx+c的表达式;
(2)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由黑色和白色正方形组成的一组有规律的图案,则第2019个图形中,黑色正方形的个数是( )

A.2019B.3027C.3028D.3029
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习指导:同学们,我们即将在“整式的加减”一章中学习同类项和合并同类项法则.同类项:所含字母相同,并且相同字母的指数也相同的项,叫做同类项,例如![]() ,3
,3![]() 和7
和7![]() 是同类项.合并同类项法则:同类项的系数相加减,所得的结果作为系数,字母和字母的指数不变.例如:
是同类项.合并同类项法则:同类项的系数相加减,所得的结果作为系数,字母和字母的指数不变.例如:![]() .请你解决下面问题,一定要化简哦。为了绿化校园,学校决定修建一块长方形草坪,长30米,宽20米,并在草坪上修建如图所示的等宽的十字路,小路宽为x米.
.请你解决下面问题,一定要化简哦。为了绿化校园,学校决定修建一块长方形草坪,长30米,宽20米,并在草坪上修建如图所示的等宽的十字路,小路宽为x米.
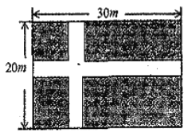
(1)用代数式表示小路和草坪的面积是多少平方米?
(2)当x=3米时,求草坪的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在2019个“口”中依次填入一列数字m1,m2,m3;……. m2019,使得其中任意四个相邻的“口”中所填的数字之和都等于-10.已知m4=0,m6=-7,则m1+m2019的值为( )
![]()
A.0B.-3C.-10D.-14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
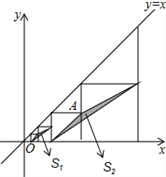
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).
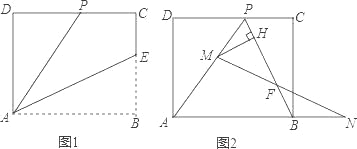
(1)求AB的长;
(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com