
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(1,﹣3),将△ABC向右平移5个单位长度,再向上平移3个单位长度得到△![]() ,其中点
,其中点 ![]() 分别是点A,B,C的对应点.
分别是点A,B,C的对应点.
(1)请你在给出的坐标系中画出![]() 和写出点A′,C′的坐标;
和写出点A′,C′的坐标;
(2)若△ABC内的一点P经过上述平移后的对应点为![]() ,用含
,用含![]() 的式子表示P点的坐标 ;(直接写出结果即可)
的式子表示P点的坐标 ;(直接写出结果即可)
(3)求△ABC的面积.

【答案】(1)图详见解析,A′(1, 2),C′(6, 0);(2)P(![]() );(3)8.5.
);(3)8.5.
【解析】
(1)根据平移规律,坐标的平移规律与图形的平移规律相同,将三个顶点坐标分别进行平移得到对应点的坐标,然后依次连线,写出点的坐标即可.
(2)根据坐标的平移规律,用平移后的点按照相反的方向进行平移,即可找到平移前的对应点.
(3)利用割补法,将三角形补成矩形,然后用矩形面积分别减去其它三角形的面积即可得到三角形ABC的面积.
解:(1)根据坐标平移规律,分别将A(﹣4,﹣1),B(﹣5,﹣4),C(1,﹣3),向右平移5个单位长度,再向上平移3个单位长度,![]()
![]() ,依次连线即可.
,依次连线即可.
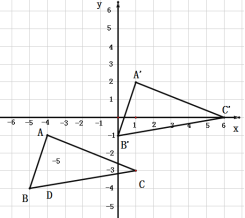
即![]()
![]()
(2)△ABC内的一点P经过上述平移后的对应点为![]() ,其平移规律为向右平移5个单位长度,再向上平移3个单位长度,所以要求P点坐标,要按照相反的方向平移,即向左平移5个单位长度,再向下平移3个单位长度,即P点坐标为(
,其平移规律为向右平移5个单位长度,再向上平移3个单位长度,所以要求P点坐标,要按照相反的方向平移,即向左平移5个单位长度,再向下平移3个单位长度,即P点坐标为(![]() )
)
(3)如图,将△ABC补成矩形BEGF,
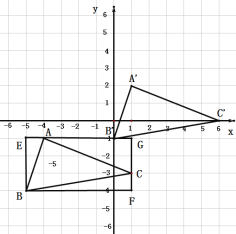
![]()


科目:初中数学 来源: 题型:
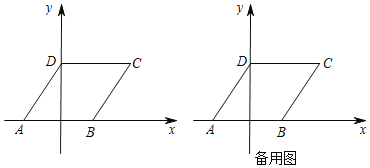
【题目】如图,ABCD在平面直角坐标系中,点A(﹣2,0),点B(2,0),点D(0,3),点C在第一象限.
(1)求直线AD的解析式;
(2)若E为y轴上的点,求△EBC周长的最小值;
(3)若点Q在平面直角坐标系内,点P在直线AD上,是否存在以DP,DB为邻边的菱形DBQP?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
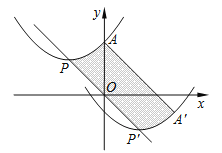
【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,∠AOC=30°,点C在AB的上方.MON为直角三角板,O为直角顶点,![]() ,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
(1)旋转开始前,∠MOC= °,∠BOM= °;
(2)运动t秒时,OM转动了 °,t为 秒时,OC与OM重合;
(3)t为何值时,∠MOC=35°?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:在函数y=|x|﹣2中,自变量x可以是任意实数;
Ⅰ如表是y与x的几组对应值.
y | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
x | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m= ;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n= ;
Ⅱ如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;根据函数图象可得:
①该函数的最小值为 ;
②该函数的另一条性质是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com