
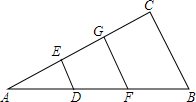
 如图,在△ABC中,点D、F是边AB上的两个动点,过点D、F分别作BC的平行线,分别交AC于点E、G.记△ADE的面积为S1,四边形DEGF的面积为S2,四边形FGCB的面积为S3.
如图,在△ABC中,点D、F是边AB上的两个动点,过点D、F分别作BC的平行线,分别交AC于点E、G.记△ADE的面积为S1,四边形DEGF的面积为S2,四边形FGCB的面积为S3.分析 (1)由点D、E、F、G分别是边AB、AC的三等分点,可得DF∥EG∥BC,AD:AE:AB=1:2:3,即可证得△ADF∽△AEG∽△ABC,然后由相似三角形面积比等于相似比的平方,求得S△ADF:S△AEG:S△ABC的值,继而求得答案;
(2)过点A作AH⊥BC于H,AH交DE于M、交FG于N,如图所示:设ED=a,GF=b,AM=h,则BC=a+b,由△AED∽△AFG,得到$\frac{AM}{AN}$=$\frac{DE}{FG}$,于是求得AN=$\frac{b}{a}$h,MN=($\frac{b}{a}$-1)h,求出图形的面积S1=$\frac{1}{2}$ah,S2=$\frac{1}{2}$(a+b)($\frac{b}{a}$-1)h,S3=$\frac{1}{2}$(b+a+b)h,由于S1+S2=S3,于是得到方程$\frac{1}{2}$ah+$\frac{1}{2}$(a+b)($\frac{b}{a}$-1)h=$\frac{1}{2}$(b+a+b)h,得到b=(1+$\sqrt{2}$)a,根据平行线分线段成比例得到AG:AE=1+$\sqrt{2}$,等量代换即可得到结论.
解答 解:(1)∵AD=DF=FB,
∵DE∥FG∥BC,∴AD:AF:AB=1:2:3,
∴△ADE∽△AFG∽△ABC,
∴S△ADE:S△AFG:S△ABC=1:4:9,
∴S1:S2:S3=1:3:5.
(2)过点A作AH⊥BC于H,AH交DE于M,交FG于N,如图所示:
设ED=a,GF=b,AM=h,
则BC=a+b,
∵DE∥FG,
∴△AED∽△AFG,
∴$\frac{AM}{AN}$=$\frac{DE}{FG}$,
∴AN=$\frac{b}{a}$h,MN=($\frac{b}{a}$-1)h,
∴S1=$\frac{1}{2}$ah,S2=$\frac{1}{2}$(a+b)($\frac{b}{a}$-1)h,S3=$\frac{1}{2}$(b+a+b)h,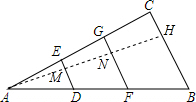
∵S1+S2=S3,
∴$\frac{1}{2}$ah+$\frac{1}{2}$(a+b)($\frac{b}{a}$-1)h=$\frac{1}{2}$(b+a+b)h,
解得:b=(1+$\sqrt{2}$)a,
∴AG:AE=1+$\sqrt{2}$,
∴$\frac{EG}{AE}$=$\sqrt{2}$,
∵AD=BF,DE∥GF∥BC,
∴EG:GC=$\sqrt{2}$.
点评 此题主要考查的是相似三角形的判定和性质,理解相似三角形的面积比等于相似比的平方是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
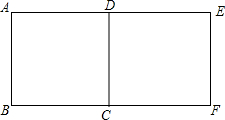 如图所示,图中的两个正方形可以通过平移的方法互相得到,如果将其中一个正方形绕某个点旋转一个角度后能与另一个重合,问:这样的点共有几个?请在图中分别标出它们.
如图所示,图中的两个正方形可以通过平移的方法互相得到,如果将其中一个正方形绕某个点旋转一个角度后能与另一个重合,问:这样的点共有几个?请在图中分别标出它们.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com