[题目]如图.为的直径.为上一点..延长至点.使得.过点作.垂足在的延长线上.连接.(1)求证:是的切线,(2)当时.求图中阴影部分的面积. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，为的直径，为上一点，，延长至点，使得，过点作，垂足在的延长线上，连接.

（1）求证：是的切线；

（2）当时，求图中阴影部分的面积.

【答案】（1）详见解析；（2）.

【解析】

（1）连接OB，欲证是的切线，即要证到∠OBE=90°，而根据等腰三角形的性质可得到.再根据直角三角形的性质可得到，从而得到，从而得到，然后根据切线的判定方法得出结论即可.

（2）先根据已知条件求出圆的半径，再根据扇形的面积计算公式计算出扇形OBC的面积，再算出三角形OBC的面积，则阴影部分的面积可求.

（1）证明：如图，连接

∵,,

∴.

∵,,

∴在中，.

∴

∴在中，.

∴，即.

又∵为圆上一点，

∴是圆的切线.

（2）解：当时，.

∵为圆的直径，

∴.

又∵，

∴.

在中，，即，

解得.

∴，

∴

练习册系列答案

本土教辅名校学案黄冈期末全程特训卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

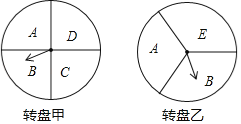
【题目】某超市在端午节期间开展优惠活动，凡购物者可以通过转动转盘的方式享受折扣优惠，本次活动共有两种方式，方式一：转动转盘甲，指针指向A区域时，所购买物品享受9折优惠、指针指向其它区域无优惠；方式二：同时转动转盘甲和转盘乙，若两个转盘的指针指向每个区域的字母相同，所购买物品享受8折优惠，其它情况无优惠．在每个转盘中，指针指向每个区城的可能性相同（若指针指向分界线，则重新转动转盘）

（1）若顾客选择方式一，则享受9折优惠的概率为多少；

（2）若顾客选择方式二，请用树状图或列表法列出所有可能，并求顾客享受8折优惠的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣+bx+c经过A，B两点．

（1）求抛物线的解析式；

（2）点P在抛物线上，点Q在直线AB上，当P，Q关于原点O成中心对称时，求点Q的坐标；

（3）点M为直线AB上的动点，点N为抛物线上的动点，当以点O、B、M、N为顶点的四边形是平行四边形时，请直接写出点M的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】按如下方法，将△ABC的三边缩小的原来的，如图，任取一点O，连AO、BO、CO，并取它们的中点D、E、F，得△DEF，则下列说法正确的个数是（　　）

①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形

③△ABC与△DEF的周长比为1：2④△ABC与△DEF的面积比为4：1．

A. 1B. 2C. 3D. 4

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，CA＝CB＝5，AB＝6，AB⊥y轴，垂足为A．反比例函数y＝（x＞0）的图象经过点C，交AB于点D．

（1）若OA＝8，求k的值；

（2）若CB＝BD，求点C的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校九年级数学兴趣小组在测量某市建筑物CD的高度时，他们在A处测得建筑物顶部D处的仰角为49°，然后他们往CA方向后退了3.4米到达B处（C，A，B在一条直线上），测得建筑物顶部D的仰角恰好为45°，请用他们测量的数据求出建筑物CD的高度．（结果精确到0.1m，参考数据sin49°≈0.75，cos49°≈0.66，tan49°≈1.15）．