Question

已知⊙O和⊙O上的一点A(如图)．

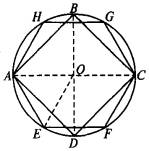
(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH；

(2)在(1)题的作图中，如果点E在上，求证：DE是⊙O内接正十二边形的一边．

 

Answer 1

答案：
解析：

(1)作法：①作直径AC． ②作直径BD⊥AC． ③依次连结A、B、C、D四点． 四边形ABCD即为⊙O的内接正方形． ④分别以A、C为圆心，OA长为半径作弧，交⊙O于E、H、F、G． ⑤顺次连结A、E、F、C、G、H各点． 六边形AEFCGH即为⊙O的内接正六边形． (2)证明：连结OE、DE． ∵　∠AOD==90°，∠AOE==60°， ∴　∠DOE=∠AOD-∠AOE=30°． ∴　DE为⊙O的内接正十二边形的一边．

提示：

求作⊙O的内接正六边形和正方形，依据定理应将⊙O的圆周六等分、四等分，而正六边形的边长等于半径；互相垂直的两条直径由垂径定理知把圆四等分．要证明DE是⊙O内接正十二边形的一边，由定理知，只需证明DE所对圆心角等于360°÷12=30°．