
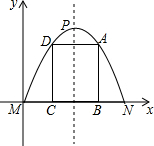 如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系,
如图,有一块铁皮,拱形边缘呈抛物线状,MN=4dm,抛物线顶点到MN的距离是4dm.要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在MN上,A、D落在抛物线上.建立如图所示的平面直角坐标系,分析 (1)根据MN=4dm,抛物线顶点到MN的距离是4dm,得到N(4,0),P(2,4),即可求得函数的解析式;
(2)由OC=1dm,求得D的横坐标是1,根据函数的解析式得到y=3,求出D(1,3),由于A,D关于对称轴对称,于是得到AD=2,然后根据矩形的周长公式即可得到结论.
解答 解:(1)∵MN=4dm,抛物线顶点到MN的距离是4dm,
∴N(4,0),P(2,4),
设抛物线的解析式为:y=a(x-2)2+4,
把N(4,0)代入得:0=a(4-2)2+4,
解得:a=-1,
∴抛物线的解析式为:y=-(x-2)2+4,
即:抛物线的解析式为:y=-x2+4x;
(2)∵OC=1dm,
∴D的横坐标是1,
∴y=3,
∴D(1,3),
∵A,D关于对称轴对称,
∴AD=2,
∵四边形ABCD是矩形,
∴BC=AD=2,
CD=AB=3,
∴矩形ABCD的周长为10dm.
点评 此题考查了二次函数的应用,把一个实际问题转化成数学问题,需要观察分析、建模,建立直角坐标系下的函数模型是解决实际问题的常用方法,同一问题有不同的建模方式,通过分析比较可获得简解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
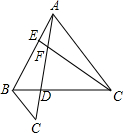 如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:
如图,已知等边△ABC,AE=BD,CE、AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=1,c=2 | B. | a=1,b=-1,c=-2 | C. | a=1,b=1,c=-2 | D. | a=1,b=-1,c=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 1≤x<45 | 45≤x≤80 |
| 售价(元/件) | x+40 | 80 |
| 每天销量(件) | 200-2x | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:选择题
用配方法解方程x2+8x+7=0,则配方正确的是( )
A.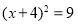 B.
B.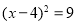 C.
C.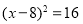 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com