
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() ,
,![]() ,且以
,且以![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.

(1)直接写出![]() 点的坐标;
点的坐标;
(2)请用无刻度直尺作直线![]() ,使直线
,使直线![]() 经过点
经过点![]() 且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
(3)已知点![]() 是
是![]() 边上一点,若线段
边上一点,若线段![]() 将菱形
将菱形![]() 的面积分为
的面积分为![]() 两部分,直接写出点
两部分,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)算出AB,AC,BC,根据菱形的性质找到点D即可;
(2)连接AC和BD交于Q,画直线PQ即为直线l;
(3)计算出菱形ABCD的面积,从而得出分割成的两部分的面积,设T的坐标为(4,m),再利用梯形的面积公式求解即可.
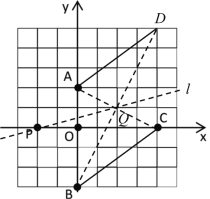
解:(1)![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点的四边形为菱形,
为顶点的四边形为菱形,
可知:AB=5,AC=![]() ,BC=5,
,BC=5,
∴该菱形以AB和BC为边,
则点D的坐标为:(4,5);
(2)如图,连接![]() 、
、![]() 交于点
交于点![]() ,直线
,直线![]() 即直线
即直线![]() ;
;
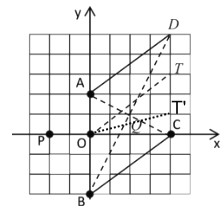
(3)由(2)可得:菱形ABCD的面积= 5×4=20,20×![]() =8,
=8,
则线段OT将菱形面积分为8和12两个部分,
设T的坐标为(4,m),则DT=5-m,CT=m,
则S梯形AOTD=![]() ×(2+5-m)×4=8,
×(2+5-m)×4=8,
或S梯形AOTD=![]() ×(2+5-m)×4=12,
×(2+5-m)×4=12,
解得:m=3或m=1,
∴![]() 或
或![]()


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
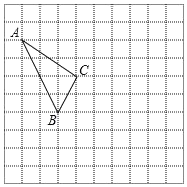
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,4),(﹣1,2).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)将△ABC向右平移2个单位长度,然后再向下平移3个单位长度,得到△A′B′C′,画出平移后的△A′B′C′.
(3)求S△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上(不与点
上(不与点![]() 重合)的任意一点,连接
重合)的任意一点,连接![]() ,并使
,并使![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,设
,设![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的度数;
的度数;
(3)若![]() 的三边垂直平分线的交点在该三角形的内部,直接写出
的三边垂直平分线的交点在该三角形的内部,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为6个单位长度,点
的边长为6个单位长度,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,以1个单位/秒的速度按
出发,以1个单位/秒的速度按![]() 的方向运动,再次回到
的方向运动,再次回到![]() 点结束运动,设
点结束运动,设![]() 点运动的时间为
点运动的时间为![]() 秒.
秒.

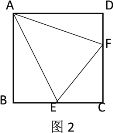

(1)如图1,若![]() 为直角三角形,求
为直角三角形,求![]() 的值;
的值;
(2)如图2,若点![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,点![]() 是对角线
是对角线![]() 的三等分点,且
的三等分点,且![]() ,若
,若![]() ,直接写出满足条件的
,直接写出满足条件的![]() 点的个数,并注明这些
点的个数,并注明这些![]() 点分别在正方形的哪条边上.
点分别在正方形的哪条边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料(1),并利用(1)的结论解决问题(2)和问题(3).
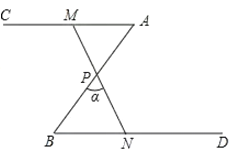
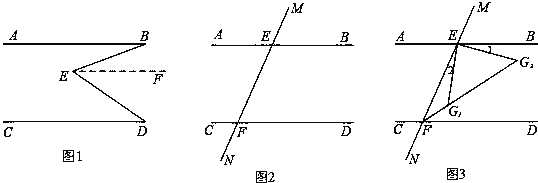
(1)如图1,AB∥CD,E为形内一点,连结BE、DE得到∠BED,求证:∠E=∠B+∠D
悦悦是这样做的:
过点E作EF∥AB.则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
(2)如图2,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(3)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2,求证:∠FG1E+∠G2=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 经过第一、二、三象限,与
经过第一、二、三象限,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在这条直线上,连接
在这条直线上,连接![]() ,已知
,已知![]() 的面积等于1.
的面积等于1.

(1)求![]() 的值;
的值;
(2)如果反比例函数y=![]() (k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
(k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,点A,B,E分别是x轴和y轴上的任意点. BD是∠ABE的平分线,BD的反向延长线与∠OAB的平分线交于点C.
探究: (1)求∠C的度数.
发现: (2)当点A,点B分别在x轴和y轴的正半轴上移动时,∠C的大小是否发生变化?若不变,请直接写出结论;若发生变化,请求出∠C的变化范围.
应用:(3)如图2在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC外角的平分线相交于点P,求∠P的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O,A在数轴上表示的数分别是0,l,将线段OA分成1000等份,其分点由左向右依次为M1,M2…M999;将线段OM1分成1000等份,其分点由左向右依次为N1,N2…N999;将线段ON1分成1000等份,其分点由左向右依次为P1,P2…P999.则点P314所表示的数用科学记数法表示为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
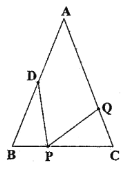
(1)如果点![]() 在线段
在线段![]() 上以
上以![]() 厘米
厘米![]() 秒的速度由
秒的速度由![]() 向
向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.
点运动.
①若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,
的运动速度相等,![]() 秒钟时,
秒钟时,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
②点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() ?并说明理由;
?并说明理由;
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以原来运动速度从点
以原来运动速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 的三边运动,求多长时间点
的三边运动,求多长时间点![]() 与点
与点![]() 第一次在
第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com