
【题目】完成下面的证明过程
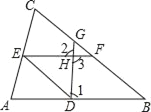
如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(________),
∴∠1+∠3=180°
∴______∥______(________)
∴∠B=______(________)
∵∠B=∠DEF(已知)
∴∠DEF=______(等量代换)
∴DE∥BC(________)
【答案】对顶角相等 EF AB 同旁内角互补,两直线平行 ∠CFE 两直线平行,同位角相等 ∠CFE 两直线平行
【解析】
先由对顶角相等可得:∠2=∠3,然后由∠1+∠2=180°,根据等量代换可得:∠1+∠3=180°,然后根据同旁内角互补两直线平行可得:EF∥AB,然后根据两直线平行同位角相等可得:∠B=∠CFE,然后由∠B=∠DEF,根据等量代换可得:∠CFE=∠DEF,然后根据内错角相等两直线平行即可得到:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(对顶角相等),
∴∠1+∠3=180°
∴EF∥AB(同旁内角互补,两直线平行)
∴∠B=∠CFE(两直线平行,同位角相等)
∵∠B=∠DEF(已知)
∴∠DEF=∠CFE(等量代换)
∴DE∥BC(内错角相等,两直线平行).


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( ) 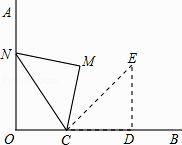
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点P在函数y= ![]() (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )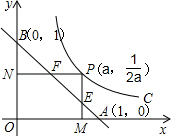
A.4
B.2
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )

A. 10 ° B .20 ° C .30° D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) 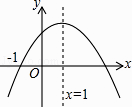
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①所示,试说明OB∥AC;
(2)如图②,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可);
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(4)在(3)的条件下,在平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA的度数等于________(在横线上填上答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
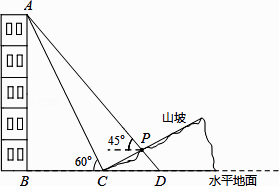
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度为 ![]() (即tan∠PCD=
(即tan∠PCD= ![]() ).
).
(1)求该建筑物的高度(即AB的长).
(2)求此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.
(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com