
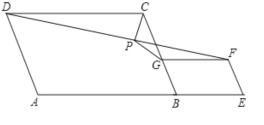
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A、 B、 E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
可通过构建全等三角形求解.延长GP交DC于H,可证三角形DHP和PGF全等,已知的有DC∥GF,根据平行线间的内错角相等可得出两三角形中两组对应的角相等,又有DP=PF,因此构成了全等三角形判定条件中的(AAS),于是两三角形全等,那么HP=PG,可根据三角函数来得出PG、CP的比例关系.
延长GP交DC于点H,

∵AB=AD,BG=BE,
∴平行四边形ABCD和平行四边形BEFG都是菱形,
∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH
∴△CHG是等腰三角形,
∴PG⊥PC,(三线合一)
又∵∠ABC=∠BEF=60°,
∴∠GCP=60°,
∴![]() =
=![]() .
.
故选B.


科目:初中数学 来源: 题型:
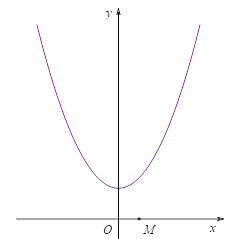
【题目】将抛物线![]() 向左平移2个单位,再向上平移4个单位得到一个新的抛物线.
向左平移2个单位,再向上平移4个单位得到一个新的抛物线.
(1)求新的抛物线的解析式.
(2)过![]() 作直线
作直线![]() ,使得直线
,使得直线![]() 与新的抛物线仅有一个公共点,求直线
与新的抛物线仅有一个公共点,求直线![]() 的解析式及相应公共点的坐标.
的解析式及相应公共点的坐标.
(3)请猜想在新的抛物线上是否有且仅有四个点![]() 、
、![]() 、
、![]() 、
、![]() 使得
使得![]() 、
、![]() 、
、![]() 、
、![]() 分别与(2)中的所有公共点所围成的图形的面积均为S?若有,请求出S并直接写出
分别与(2)中的所有公共点所围成的图形的面积均为S?若有,请求出S并直接写出![]() 、
、![]() 、
、![]() 、
、![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣kx+m与双曲线y=![]() (x>0)交于A、B两点,点A的横坐标为1,点B的纵坐标为2,点P是y轴上一动点,当△PAB的周长最小时,点P的坐标是_______.
(x>0)交于A、B两点,点A的横坐标为1,点B的纵坐标为2,点P是y轴上一动点,当△PAB的周长最小时,点P的坐标是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
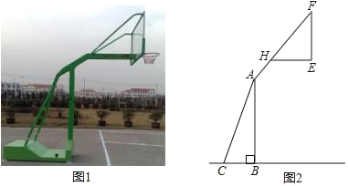
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60m,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1m,HF段的长为1.50m,篮板底部支架HE的长为0.75m.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板顶端F到地面的距离.(结果精确到0.1 m;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
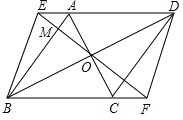
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点O作一条直线分别交DA,BC的延长线于点E,F,连接BE,DF.
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,![]() ,AE=2,求菱形ABCD的边长.
,AE=2,求菱形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0 的两根 x1,x2均为正数,其中x1>x2,且满足1<x1﹣x2<2,那么称这个方程有“友好根”.
(1)方程(x﹣![]() )(x﹣
)(x﹣![]() )=0_____“友好根”(填:“有”或“没有”);
)=0_____“友好根”(填:“有”或“没有”);
(2)已知关于x的 x2﹣(t﹣1)x+t﹣2=0有“友好根”,求 t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
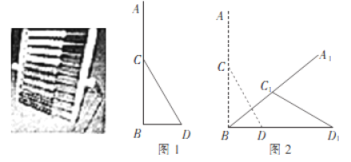
【题目】如图所示的益智玩具由一块主板AB和一个支撑架CD组成,其侧面示意图如图1所示,测得AB⊥BD,AB=40cm,CD=25cm,点C为AB的中点.现为了方便儿童操作,需调整玩具的摆放,将AB绕点B顺时针旋转,CD绕点C旋转,同时点D做水平滑动(如图2),当点C1到BD的距离为10cm时停止运动,求点A经过的路径的长和点D滑动的距离.(结果保留整数,参考数据:![]() ≈1.732,
≈1.732, ![]() ≈4.583,π≈3.142)
≈4.583,π≈3.142)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).

(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使![]() ≌
≌![]() ,若存在,请直接写出点F的坐标;若不存在,请说明理由;
,若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q.试探究:当m为何值时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com