
����Ŀ�����ֿ�������������й��ɵ�ͼ�ν��м���ʱ����Щ����Բ��á��ֿ�������ķ�����
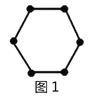
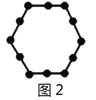
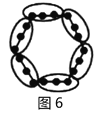
���磺ͼ1��6���㣬ͼ2��12���㣬ͼ3��18���㣬�������˹��ɣ���ͼ8��ͼ![]() �ж��ٸ��㣿
�ж��ٸ��㣿
���ǽ�ÿ��ͼ�ηֳ���ȫ��ͬ��6�飬ÿ��ڵ�ĸ�����ͬ����ͼ��������ͼ1�кڵ������![]() ����ͼ2�кڵ������
����ͼ2�кڵ������![]() ����ͼ3�кڵ������
����ͼ3�кڵ������![]() �������������������ͼ8��ͼ
�������������������ͼ8��ͼ![]() �кڵ�ĸ����ֱ���______��_________��
�кڵ�ĸ����ֱ���______��_________��

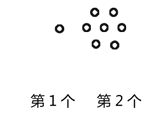
����ο����ϡ��ֿ�����������Ƚ�����ĵ�����зֿ飨���ڴ���ϣ���������������⣺
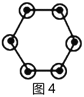
��1����6����������______��ԲȦ����![]() ����������______��ԲȦ��
����������______��ԲȦ��
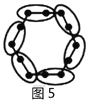
��2��СԲȦ�ĸ��������331��������ǵڼ�������


���𰸡�48��6n����1��91��![]() ����2�����11������
����2�����11������
��������
���ݹ��ɿ����ͼ8�кڵ������ͼn�кڵ������
��1����2��ͼ��2Ϊһ�飬��Ϊ3�飬��1����3��ͼ��3Ϊһ�飬��Ϊ6�飬��1�����˹��ɵã���6��������6Ϊһ�飬��Ϊ15�飬��1���õ�n���������У�n��3��n-1��+1=3n2-3n+1��
��2����3n2-3n+1=331�������н�����������ĵ��ݴ˽��.
�⣺ͼ8�кڵ������6��8=48����ͼn�кڵ������6n����
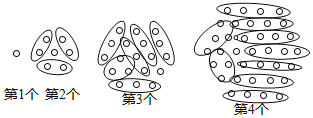
��1����ͼ��ʾ����1���������У�1����
��2����������2��3+1=7����
��3����������3��6+1=19����
��4����������4��9+1=37����
��5����������5��12+1=61����
��6����������6��15+1=91����
��
��n����������n��3��n-1��+1=3n2-3n+1��
�ʴ�Ϊ��91��3n2-3n+1��
��2��3n2-3n+1=331��
n2-n-110=0��
��n-11����n+10��=0��
n1=11��n2=-10���ᣩ��
��СԲȦ�ĸ��������331�����ǵ�11������


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ݹ�˾Ϊ��߿�ݷּ���ٶȣ���������������������˹��ּ������ͺŵĻ����˵Ĺ���Ч�ʺͼ۸������
�ͺ� | �� | �� |
ÿ̨ÿСʱ�ּ��ݼ���(��) | 1000 | 800 |
ÿ̨�۸�(��Ԫ) | 5 | 3 |
�ù�˾�ƻ������������ͺŵĻ����˹�10̨������ʹ��10̨������ÿСʱ�ּ��ݼ����ܺͲ�����8500��
(1)�蹺������ͺŵĻ�����x̨��������10̨�����������ķ���Ϊy��Ԫ����y��x֮��Ĺ�ϵʽ��
(2)����̨�����ͺŵĻ����ˣ���ʹ������10̨�����������ܷ������٣����ٷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijƷ�Ƶ������۹�˾��Ӫ��Ա14�ˣ����۲�Ϊ�ƶ�Ӫ����Ա�����۵��Զ��ͳ������14��ij�µ����������£���λ��̨����
������ | 200 | 170 | 130 | 80 | 50 | 40 |
���� | 1 | 1 | 2 | 5 | 3 | 2 |
��1���ù�˾Ӫ��Ա���۸�Ʒ�Ƶ��Ե�������ƽ������ ̨����λ���� ̨�������� ̨��
��2�����۲�������ÿλӪ��Ա����������Ϊ90̨������Ϊ�Ƿ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣩��a+b��10����ab�����ֵ�Ƕ��٣�
��̽����
̽��һ����a��b��0ʱ����abֵ��
��Ȼ��ʱ��a��b��5����ab��5��5��25
̽��������a��b����1ʱ����abֵ��
��a��b��1����a��b+1��
����֪��b+1+b��10
��� b��![]() ��
��
a��b+l��![]() +1��
+1��![]()
��ab��![]() ��
��![]()
��a��b����1����b��a��1�������ɵã�b��![]() ��a��
��a��![]()
��ab��![]() ��
��![]() ��
��
̽��������a��b����2ʱ����abֵ����������������д��̽�����̣���
̽���ģ�����±���
a��b | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
ab | �� | �� �� | �� �� |
| 25 |
| �� �� | �� �� | �� |
�����ۣ���a+b��10����ab�����ֵ���� �����۲��������ֱ��д���������
����չ����a+b��m����ab�����ֵ���� ����
��Ӧ�ã���һ����Ϊ12m����˿Χ��һ�������Σ������������������ֵ���� ��m2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ�A��B��C��������ʾ�����ֱ�Ϊa��b��1����|a��1|+|b��1|��|a��b|��������ѡ���У�����A��B��C����λ�ù�ϵ������Ϊ��������
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
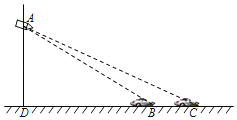
����Ŀ����ͼ��һ���γ��ھ���ij·�ڵĸ�Ӧ��B��C��ʱ�����۵Ƹ��ϵĵ��Ӿ������㵽������Ƭ������Ӧ��֮�����BCΪ6m���ڸ�Ӧ��B��C������õ��Ӿ���A�����Ƿֱ�Ϊ��ABD��18������ACD��14��������Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij���
���ο����ݣ�sin14���0.242��cos14���0.97��tan14���0.25��sin18���0.309��cos18���0.951��tan18���0.325��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
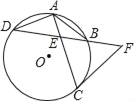
����Ŀ����ͼ��ʾ����O�У���AC��BD����E��![]() ��
��
��1����֤��![]() ��
��
��2���ӳ�EB��F��ʹEF��CF�����ж�CF����O��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
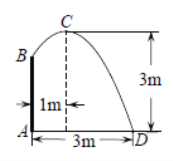
����Ŀ����ͼ������ˮ�ص�����![]() ����ֱ��װһ��ˮ��
����ֱ��װһ��ˮ��![]() ��ˮ�ܵĶ��˰���һ����ˮͷ��ʹ�������������ˮ�����������
��ˮ�ܵĶ��˰���һ����ˮͷ��ʹ�������������ˮ�����������![]() ��ˮƽ����Ϊ1m���ﵽ��ߵ�
��ˮƽ����Ϊ1m���ﵽ��ߵ�![]() ���߶�Ϊ3m��ˮ����ص�
���߶�Ϊ3m��ˮ����ص�![]() �������
�������![]() ��3m����ˮƽ����Ϊ
��3m����ˮƽ����Ϊ![]() �ᣬ����ƽ��ֱ������ϵ����ѡȡ��
�ᣬ����ƽ��ֱ������ϵ����ѡȡ��![]() Ϊ����ԭ��ʱ�������ߵı���ʽΪ
Ϊ����ԭ��ʱ�������ߵı���ʽΪ![]() ����ѡȡ��
����ѡȡ��![]() Ϊ����ԭ��ʱ�������߱���ʽΪ______�������Ա�����ȡֵ��Χ��______��ˮ��
Ϊ����ԭ��ʱ�������߱���ʽΪ______�������Ա�����ȡֵ��Χ��______��ˮ��![]() �ij�Ϊ______m��
�ij�Ϊ______m��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com