
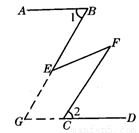
如图,已知AB∥CD,∠1=∠2,试探索∠BEF与∠EFC之间的关系,并说明理由.

∠BEF=∠EFC.
【解析】
试题分析:延长BE交CD的反向延长线于G,根据AB∥CD,得到∠1=∠G,再结合∠1=∠2,得到BE∥CF,所以∠BEF与∠EFC相等.
如答,分别延长BE、DC相交于点G.
∵AB∥CD,
∴∠1=∠G(两直线平行,内错角相等),
∵∠1=∠2,
∴∠2=∠G,
∴BE∥FC,
∴∠BEF=∠EFC(两直线平行,内错角相等).
考点:本题考查的是平行线的性质和判定
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.同时要熟练掌握平行线的性质:两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com