
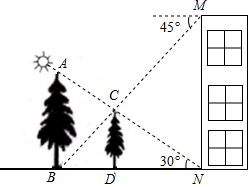
 如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)
如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号) 分析 在Rt△CDN中,由于tan30°=$\frac{CD}{DN}$,得到CD=tan30°•DN=5$\sqrt{3}$于是得到BD=CD=5$\sqrt{3}$,在Rt△ABN中,根据三角函数的定义即可得到结论.
解答  解:在Rt△CDN中,
解:在Rt△CDN中,
∵tan30°=$\frac{CD}{DN}$,
∴CD=tan30°•DN=5$\sqrt{3}$,
∵∠CBD=∠EMB=45°,
∴BD=CD=5$\sqrt{3}$,
∴BN=DN+BD=15+5$\sqrt{3}$,
在Rt△ABN中,tan30°=$\frac{AB}{BN}$,
∴AB=tan30°•BN=5+5$\sqrt{3}$,
∴树高AB是(5+5$\sqrt{3}$)米,树高CD是5$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用,解答本题的关键是借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:填空题
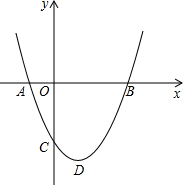 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C,在下面四个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C,在下面四个结论中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
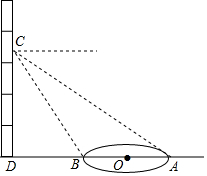 如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)
如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
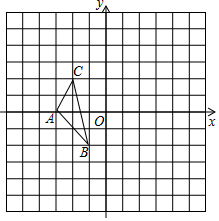 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点为A(-3,0)、B(-1,-2)、C(-2,2)和格点D(0,1).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点为A(-3,0)、B(-1,-2)、C(-2,2)和格点D(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com