【题目】如图，点
在数轴上表示的数是-8，点
在数轴上表示的数是16．若点以6个单位长度/秒的速度向右匀速运动，同时点以2个单位长度/秒的速度向左匀速运动．问：当
时，运动时间为多少秒？
A. 2秒B. 13.4秒C. 2秒或4秒D. 2秒或6秒
名师指导期末冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】(1)已知一个角的补角比它的余角的 3 倍大 30°，求这个角的度数；
(2)如图，点 C、D在线段 AB上， D是线段 AB的中点， AC 
AD ， AB6，求线段 CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC三条边的长度分别是
，
，
，记△ABC的周长为C△ABC．
（1）当x＝2时，△ABC的最长边的长度是 （请直接写出答案）；
（2）请求出C△ABC（用含x的代数式表示，结果要求化简）；
（3）我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式：S＝
．其中三角形边长分别为a，b，c，三角形的面积为S．
若x为整数，当C△ABC取得最大值时，请用秦九韶公式求出△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学习相似三角形和解直角三角形的相关内容后，张老师请同学们交流这样的一个问题：“如上图，在正方形网格上有△A1B1C1和△A2B2C2 ， 这两个三角形是否相似？”，那么你认为△A1B1C1和△A2B2C2 ， （相似或不相似）；理由是 ．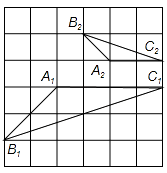 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为“有趣三角形”，这条中线称为“有趣中线”。如图，在三角形ABC中，∠C=90°，较短的一条直角边BC=1，且三角形ABC是“有趣三角形”，求三角形ABC的“有趣中线”的长。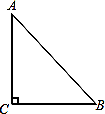
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图AB∥CD．∠1=∠2，∠3=∠4，试说明AD∥BE．
解：∵AB∥CD（已知）
∴∠4=∠ （ ）
∵∠3=∠4（已知）
∴∠3=∠ （ ）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（
即∠ =∠ （ ）
∴∠3=∠
∴AD∥BE（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠1=∠2，要得到△ABD≌△ACE，从下列条件中补选一个，则错误的是（ ）
A．AB=AC B．DB=EC C．∠ADB=∠AEC D．∠B=∠C
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A的坐标为(1，0)，以线段OA为边在第四象限内作等边三角形△AOB，点C为x正半轴上一动点(OC＞1)，连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E.
(1)求证：△OBC≌△ABD
(2)在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数;如果变化，请说明理由.
(3)当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？
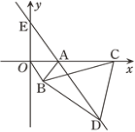
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在平面直角坐标系xOy中，O是坐标原点，点A（2，5）在反比例函数y= 
的图象上，过点A的直线y=x+b交x轴于点B．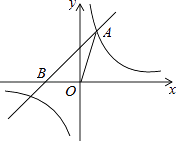
（1）求k和b的值；
（2）求△OAB的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
