练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．对方程2x2-$\frac{3}{x}$+2016=0根的情况，下列判断正确的是（　　）
    A．没有实数根B．有一个实数根C．有两个实数根D．有三个实数根

    分析 将原方程变形为2x2+2016=$\frac{3}{x}$，画出两个函数的图象，结合函数图象的交点，即可得出结论．

    解答 解：原方程可变形为2x2+2016=$\frac{3}{x}$，
    可将该方程的解看成抛物线2x2+2016的图象与反比例函数y=$\frac{3}{x}$的图象的交点，
    画出图形如下．

    结合图形即可发现两个函数图象只有一个交点，
    故选B．

    点评 本题考查了反比例函数与二次函数图象交点的问题，解题的关键是画出两函数的图象，数形结合解决问题．本题属于基础题，难度不大，解决该题型题目时，先将原方程变形，再画出两函数的图象，利用数形结合解决交点问题是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．在A、B两地之间有汽车站C站（如图1），客车由A地驶向C站，货车由B地驶向A地，两车同时出发，匀速行驶．图2是客车、货车离C站的距离y1y2（千米）与行驶时间x（小时）之间的函数关系图象．
    （1）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；
    （2）客、货两车何时相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

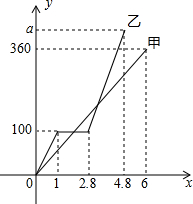    1．甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备后，乙组的工作效率提高了50%．两组各自加工零件的数量y（件）与时间x（时）的函数图象如图所示．
    （1）求甲组加工零件的数量y与时间x之间的函数关系式；
    （2）求乙组加工零件总量a的值；
    （3）甲、乙两组加工出的零件合在一起装箱，每满310件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

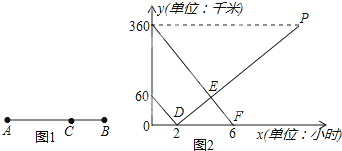
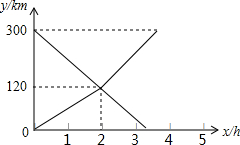    18．甲、乙两车分别从A，B两地同时出发，沿一条公路相向而行，2小时后两车相遇，相遇后乙车速度变为90km/h，而甲车速度保持不变，甲、乙两车离B地路程为y甲（km）、y乙（km），行驶时间为x（h），y甲、y乙与x之间的函数图象如图所示．
    （1）求甲车行驶完全程所用的时间；
    （2）求乙车与甲车相遇后y乙与x的函数解析式，并写出自变量x的取值范围；
    （3）当两侧相距180km时，直接写出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，以AB为直径的⊙O交△ABC的边AC于D、BC于E，过D作⊙O的切线交BC于F，交BA延长线于G，且DF⊥BC．
    （1）求证：BA=BC；
    （2）若AG=2，cosB=$\frac{3}{5}$，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A（2，2），B（-1，m）
    （1）求一次函数和反比例函数的解析式；
    （2）在给定的直角坐标系中，画出这两个函数的图象；
    （3）当x为何值时，一次函数的值大于反比例函数的值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算|-2|+2•cos60°-（-5）-（-7+3）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．先化简（$\frac{2}{x+1}$+$\frac{x+2}{{x}^{2}-1}$）÷$\frac{x}{{x}^{2}-2x+1}$，然后从不等式组$\left\{\begin{array}{l}{2x+3＞0}\\{-3x+6＞-1}\end{array}\right.$的整数解中选取一个你认为合适的数作为x的值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）（2x+5y）2；
    （2）（$\frac{1}{3}$m-$\frac{1}{2}$）2；
    （3）（-2t-1）2；
    （4）（$\frac{1}{5}$x+$\frac{1}{10}$y）2；
    （5）（7ab+2）2；
    （6）（-cd+$\frac{1}{2}$）2．

    查看答案和解析>>

    同步练习册答案