
【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图。
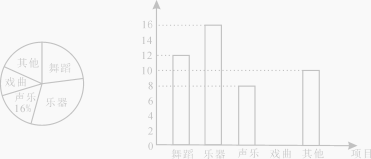
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生。其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 。扇形统计图中喜欢“戏曲”部分扇形的圆心角为 度。
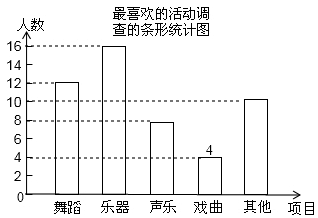
(2)请你补全条形统计图。
(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率。
【答案】(1)50,24%,28.8°;(2)详见解析;(3)![]() .
.
【解析】
试题分析:(1)用喜欢声乐的人数除以所占的百分比,进行计算即可得出一共抽查了的学生人数;喜欢“舞蹈”活动项目的人数除以被调查的总人数即可;先求出喜欢“戏曲”部分的百分比,再根据扇形所对圆心角的度数与百分比的关系是:圆心角的度数=百分比×360°,即可得出答案;(2)求出喜欢“戏曲”的人数,然后补全统计图即可;(3)列表或画出树状图,然后根据概率公式列式进行计算即可.
试题解析:(1)8÷16%=50,
![]() ×100%=24%,
×100%=24%,
100%-![]() ×100%-
×100%-![]() ×100%―16%―
×100%―16%―![]() ×100%=100%-24%-32%-16%-20%=8%
×100%=100%-24%-32%-16%-20%=8%
喜欢“戏曲”部分扇形的圆心角的度数=8%×360°=28.8°;
(2)补全条形统计图如图
(3)图表或树状图正确
画树状图如下:
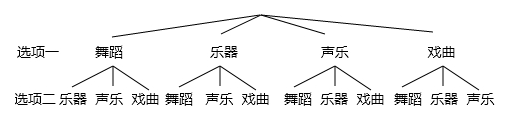
共有12种情况,其中恰好选中“舞蹈、声乐”这两项活动的有2种结果,
故恰好选中“舞蹈、声乐”这两项活动的概率是:![]() =
=![]() .
.
用列表法如下:
舞蹈 | 乐器 | 声乐 | 戏曲 | |
舞蹈 | (舞蹈、乐器) | (舞蹈、声乐) | (舞蹈、戏曲) | |
乐器 | (乐器、舞蹈) | (乐器、声乐) | (乐器、戏曲) | |
声乐 | (声乐、舞蹈) | (声乐、乐器) | (声乐、戏曲) | |
戏曲 | (戏曲、舞蹈) | (戏曲、乐器) | (戏曲、声乐) |


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为4,直线l上有一点与⊙O的圆心的距离为4,则直线l与⊙O的位置关系为( )
A. 相离 B. 相切 C. 相交 D. 相切、相交均有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用计算器求下列三角函数(保留四位小数):sin38°19′=________;cos78°43′16″=________;tan57°26′=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组为了了解某小区2000个成年人大约有多少人吸烟,随机抽查了200个成年人,结果其中有10个成年人吸烟,对于这个数据收集与处理的问题,下列说法正确的是( )
A. 该调查的方式是普查 B. 样本容量是200
C. 该小区只有190个成年人不吸烟 D. 该小区一定有100人吸烟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 交
交![]() 轴于点A,交
轴于点A,交![]() 轴于点C(0,4).抛物线
轴于点C(0,4).抛物线![]()
经过点A,交![]() 轴于点B(0,-2).点P为抛物线上一个动点,经过点P作
轴于点B(0,-2).点P为抛物线上一个动点,经过点P作![]() 轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为
轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图2,将△BDP绕点B逆时针旋转,得到△BD′P′,且旋转角∠PBP′=∠OAC,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如|5﹣3|表示5、3在数轴上对应的两点之间的距离;|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离;|5|=|5﹣0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数﹣5、﹣1、3,那么A到B的距离是 ,
A到C的距离是 . (直接填最后结果).
问题(2):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(3):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(4):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com