

分析 (1)如图1中,连接OC.只要证明△AOC是等腰直角三角形即可.
(2)由PC=x,OC=2,可得OP=$\sqrt{{x}^{2}-4}$,OE=x-$\sqrt{{x}^{2}-4}$,由四边形PCDE是菱形,推出PD⊥EC,CQ=QE,PQ=QD,由$\frac{PD}{CE}$=$\frac{PQ}{QE}$=y,推出tan∠PEQ=$\frac{PQ}{QE}$=$\frac{OC}{OE}$,由此即可解决问题.
(3)由点Q在⊙O上,∠CQP=90°,推出∠CQP所以对的弦CM是直径,由∠M+∠OPM=90°,∠QPE+∠QEP=90°,∠OPM=∠QPE,推出∠M=∠QEP,易知∠PCM=∠M,∠PCQ=∠PEQ,推出∠PCO=∠PCQ=∠CEO=30°,由此即可解决问题.
解答 解:(1)如图1中,连接OC.
∵$\widehat{AC}$=$\widehat{BC}$,
∴CO⊥AB,△AOC是等腰直角三角形,AC=$\sqrt{2}$OC=2$\sqrt{2}$,
∵四边形ACDE是菱形,
∴AE=AC=2$\sqrt{2}$,
∴BE=AB-AE=4-2$\sqrt{2}$.
(2)如图2中,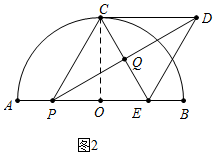
∵PC=x,OC=2,
∴OP=$\sqrt{{x}^{2}-4}$,OE=x-$\sqrt{{x}^{2}-4}$,
∵四边形PCDE是菱形,
∴PD⊥EC,CQ=QE,PQ=QD,
∵$\frac{PD}{CE}$=$\frac{PQ}{QE}$=y,
∴tan∠PEQ=$\frac{PQ}{QE}$=$\frac{OC}{OE}$,
∴y=$\frac{x-\sqrt{{x}^{2}-4}}{2}$(2≤x≤2$\sqrt{2}$).
(3)如图3中,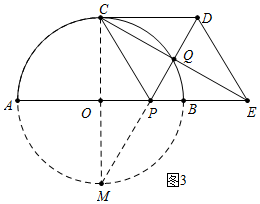
∵点Q在⊙O上,∠CQP=90°,
∴∠CQP所以对的弦CM是直径,
∵∠M+∠OPM=90°,∠QPE+∠QEP=90°,∠OPM=∠QPE,
∴∠M=∠QEP,易知∠PCM=∠M,∠PCQ=∠PEQ,
∴∠PCO=∠PCQ=∠CEO=30°,
在Rt△POC中,PC=OC÷cos30°=$\frac{4\sqrt{3}}{3}$.
点评 本题考查圆综合题、菱形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,所以中考压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段BC的两端点的坐标分别为B(3,7),C(6,3),以点A(1,0)为位似中心,将线段BC缩小为原来的$\frac{1}{2}$后得到线段DE,则端点D的坐标为( )
如图,线段BC的两端点的坐标分别为B(3,7),C(6,3),以点A(1,0)为位似中心,将线段BC缩小为原来的$\frac{1}{2}$后得到线段DE,则端点D的坐标为( )| A. | (1,$\frac{7}{2}$) | B. | (2,$\frac{7}{2}$) | C. | (1,2) | D. | (2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
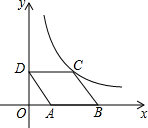 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为$\frac{56}{57}$.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为$\frac{56}{57}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:有两条边长的比值为$\frac{1}{2}$的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
定义:有两条边长的比值为$\frac{1}{2}$的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com