
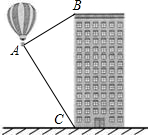
 如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )| A. | 15$\sqrt{3}$ | B. | 30$\sqrt{3}$ | C. | 45$\sqrt{3}$ | D. | 60$\sqrt{3}$ |
分析 过A作AD⊥BC,垂足为D,在直角△ABD与直角△ACD中,根据三角函数即可求得BD和CD,即可求解.
解答 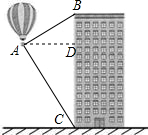 解:过A作AD⊥BC,垂足为D,
解:过A作AD⊥BC,垂足为D,
在Rt△ABD中,
∵∠BAD=30°,AD=45m,
∴BD=AD•tan30°=45×$\frac{\sqrt{3}}{3}$=15$\sqrt{3}$m,
在Rt△ACD中,
∵∠CAD=60°,AD=45m,
∴CD=AD•tan60°=45×$\sqrt{3}$=45$\sqrt{3}$m,
BC=15$\sqrt{3}$+45$\sqrt{3}$=60$\sqrt{3}$m.
故选D.
点评 本题主要考查了仰角与俯角的计算,一般三角形的计算,常用的方法是利用作高线转化为直角三角形的计算.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四川广电网络客户服务热线为96655,这五个数的众数为5和6 | |
| B. | 了解我市学生的视力情况,适宜采用抽样调查 | |
| C. | 要了解比赛选手之间成绩的稳定性,通常比较选手比赛成绩方差的大小 | |
| D. | 扇形统计图便于显示每部分扇形所对应圆心角大小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-3,1) | C. | (3,-1) | D. | (1,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
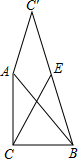 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{2}$+1 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\frac{\sqrt{5}}{2}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com