练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．（1）计算：（-1）3×5+（-2）4÷4
    （2）计算：-4÷（-$\frac{1}{2}$）2-（$\frac{3}{4}$-$\frac{1}{6}$+$\frac{5}{8}$）×24．

    分析 （1）根据有理数的混合运算的运算方法，求出算式的值是多少即可．
    （2）应用乘法分配律，求出算式的值是多少即可．

    解答 解：（1）（-1）3×5+（-2）4÷4
    =（-1）×5+16÷4
    =-5+4
    =-1

    （2）-4÷（-$\frac{1}{2}$）2-（$\frac{3}{4}$-$\frac{1}{6}$+$\frac{5}{8}$）×24
    =-4÷$\frac{1}{4}$-$\frac{3}{4}$×24+$\frac{1}{6}$×24-$\frac{5}{8}$×24
    =-16-18+4-15
    =-45

    点评 此题主要考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．已知二次函数y=mx2-5mx+1（m为常数，m＞0），设该函数的图象与y轴交于点A，该图象上的一点B与点A关于该函数图象的对称轴对称．
    （1）求点A，B的坐标；
    （2）点O为坐标原点，点M为该函数图象的对称轴上一动点，求当M运动到何处时，△MAO的周长最小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35°，求∠AOD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，有一座拱桥是圆弧形，它的跨度AB=60米，拱高PD=18米．
    （1）求圆弧所在的圆的半径r的长；
    （2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE=4米时，是否要采取紧急措施？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

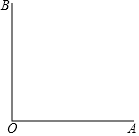    19．如图，已知∠AOB=90°，射线0A绕点O逆时针方向以毎秒6°的速度旋转（当旋转角度等于360°时，OA停止旋转），同时0B绕点O以每秒2°的速度旋转（当OA停止旋转时，OB同样 停止旋转）．求当OA旋转多少秒，旋转后的OA与OB形成的角度为50°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）计算：（$\sqrt{2}$+1）-$\sqrt{2}$tan45°+|-$\sqrt{2}$|；
    （2）解方程：x2-2$\sqrt{3}$x+3=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知关于x的分式方程$\frac{3x}{x-6}$-2=$\frac{m}{x-6}$的解是正数，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，一次函数y1=kx+b的图象与x轴、y轴分别交于点A、B，与一次函数y2=x的图象交于点M，点A的坐标为（6，0），点M的横坐标为2，过点P（a，0），作x轴的垂线，分别交函数y=kx+b和y=x的图象于点C、D．
    （1）求一次函数y1=kx+b的表达式；
    （2）若点M是线段OD的中点，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在△ABC中，AD⊥BC，垂足为D，AD=4，BD=2，CD=8．
    （1）求证：∠BAC=90°；
    （2）P为BC边上一点，连接AP，若△ABP为等腰三角形，请求出BP的长．

    查看答案和解析>>

    同步练习册答案