
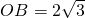 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折 痕为BE.
痕为BE.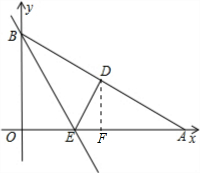 解:(1)过点D作DF⊥OA,垂足为F,因为Rt△AOB沿BE折叠时,OB边落在AB边上,点O与点D重合,
解:(1)过点D作DF⊥OA,垂足为F,因为Rt△AOB沿BE折叠时,OB边落在AB边上,点O与点D重合, =
= ,OF=
,OF=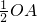 =3,
=3, ).
). ))入y=ax2+bx,
))入y=ax2+bx,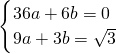 .
. .
.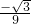 x2+
x2+ x.
x. ,∠OAB=30°,根据锐角三角函数的定义可计算出A,B两点的坐标,根据三角形全等及三角形内角与外角的关系可知∠BEO=60°,BD=
,∠OAB=30°,根据锐角三角函数的定义可计算出A,B两点的坐标,根据三角形全等及三角形内角与外角的关系可知∠BEO=60°,BD= AB,再根据锐角三角函数的定义及三角形中位线定理即可求出D、E两点的坐标.
AB,再根据锐角三角函数的定义及三角形中位线定理即可求出D、E两点的坐标.

科目:初中数学 来源: 题型:
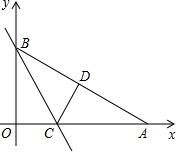 如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=
如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
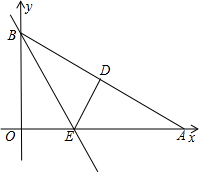 痕为BE.
痕为BE.查看答案和解析>>
科目:初中数学 来源: 题型:
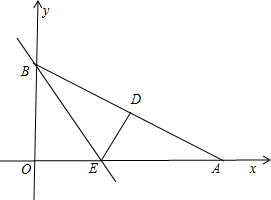 重合,点A在x轴上,点B在y轴上OB=
重合,点A在x轴上,点B在y轴上OB=| 3 |
查看答案和解析>>
科目:初中数学 来源:山东省中考真题 题型:解答题
 ,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com