
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
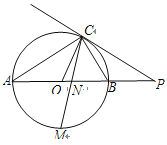
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、8.
【解析】
试题分析:(1)、根据OA=OC得出∠A=∠ACO,根据∠COB=2∠A,,∠COB=2∠PCB,则∠A=∠ACO=∠PCB,根据AB为直径得出∠ACO+∠OCB=90°,则∠PCB+∠OCB=90°,得出切线;(2)、根据AC=PC得出∠A=∠P,则∠A=∠ACO=∠PCB=∠P,根据∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB得出∠COB=∠CBO,然后得出答案;(3)、连接AM、BM,根据M是弧的中点得出∠ACM=∠BCM,根据∠ACM=∠ABM得到∠BCM=∠ABM,从而得出△MBN∽△MCB,根据相似比得出BM2=MN![]() MC;根据等腰直角△ABM中AB的长度得出AM和BM的长度,然后计算.
MC;根据等腰直角△ABM中AB的长度得出AM和BM的长度,然后计算.
试题解析:(1)、如图∵OA=OC,∴∠A=∠ACO,
又∵∠COB=2∠A,∠COB=2∠PCB,∴∠A=∠ACO=∠PCB,又∵AB是⊙O的直径, ∴∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,∴∠PCO=90°,即OC⊥CP, 而OC是⊙O的半径,∴PC是⊙O的切线;.
(2)、∵AC=PC,∴∠A=∠P, ∴∠A=∠ACO=∠PCB=∠P, 又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,∴BC=OC,∴BC=![]() AB;
AB;
(3)、连接MA,MB,

∵点M是弧AB的中点, ∴![]() ,∴∠ACM=∠BCM,∵∠ACM=∠ABM,∴∠BCM=∠ABM,
,∴∠ACM=∠BCM,∵∠ACM=∠ABM,∴∠BCM=∠ABM,
又∵∠BMN=∠BMC,∴△MBN∽△MCB,∴![]() , ∴BM2=MN
, ∴BM2=MN![]() MC,
MC,
又∵AB是⊙O的直径,![]() ,∴∠AMB=90°,AM=BM,
,∴∠AMB=90°,AM=BM,
∴AB=4,∴BM=2![]() ,∴MN
,∴MN![]() MC=BM2=(2
MC=BM2=(2![]() )2=8
)2=8


科目:初中数学 来源: 题型:
【题目】某商店出售两件衣服,每件卖了200元,其中一件赚了25%,而另一件赔了20%,那么商店在这次交易中( )
A. 赚了10元 B. 亏了10元 C. 赚了20元 D. 亏了20元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )
A.20 B.1508 C.1550 D.1558
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市同价销售同一款可拆分式驱蚊器,1套驱蚊器由1个加热器和1瓶电热蚊香液组成.电热蚊香液作为易耗品可单独购买,1瓶电热蚊香液的售价是1套驱蚊器的![]() .已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
.已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
(1)求1套驱蚊器和1瓶电热蚊香液的售价;
(2)为了促进该款驱蚊器的销售,甲超市打8.5折销售,而乙超市采用的销售方法是顾客每买1套驱蚊器送1瓶电热蚊香液.在这段促销期间,甲超市销售2000套驱蚊器,而乙超市在驱蚊器销售上获得的利润不低于甲超市的1.2倍.问乙超市至少销售多少套驱蚊器?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com