
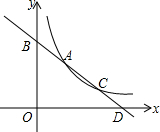
 如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).
如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).分析 (1)首先由一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b),求得a与b的值,继而求得点B,C,D的坐标,再由S△OAC=S△BOD-S△OAB-S△OCD求得答案;
(2)分别从若∠AOP=90°与若∠OAP=90°,利用相似三角形的性质,即可求得点P的坐标.
解答 解:(1)如图1,连接OA,OC,
∵点A(2,2$\sqrt{3}$)在反比例函数y=$\frac{a}{x}$的图象上,
∴a=xy=2×2$\sqrt{3}$=4$\sqrt{3}$,
∵点C(4,b)在反比例函数y=$\frac{a}{x}$的图象上,
∴b=$\frac{4\sqrt{3}}{4}$=$\sqrt{3}$,
∴点C(4,$\sqrt{3}$),
∵一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与x,y轴的交点分别为D,B,
∴D(6,0),B(0,3$\sqrt{3}$),
∴S△OAC=S△BOD-S△OAB-S△OCD=$\frac{1}{2}$×6×3$\sqrt{3}$-$\frac{1}{2}$×3$\sqrt{3}$×2-$\frac{1}{2}$×6×$\sqrt{3}$=3$\sqrt{3}$;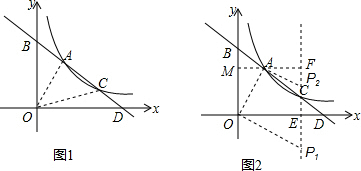 (2)存在.
(2)存在.
如图2,过点A作AM⊥x轴于点M,设直线m交x轴于点E,
∵C(4,$\sqrt{3}$),A(2,2$\sqrt{3}$),
∴OE=4,OM=2$\sqrt{3}$,AM=2,
①若∠AOP=90°,则∠AOE+∠EOP=90°,
∵∠AOM+∠AOE=90°,
∴∠AOM=∠EOP,
∵∠AMO=∠OEP=90°,
∴△AOM∽△POE,
∴$\frac{OM}{OE}=\frac{AM}{EP}$,
∴$\frac{2\sqrt{3}}{4}=\frac{2}{EP}$,
解得:EP=$\frac{4\sqrt{3}}{3}$,
∴P1(4,-$\frac{4\sqrt{3}}{3}$);
②若∠OAP=90°,过点A作AF⊥m于点F,
则∠AOM=∠FAP=90°-∠OAM,∠AMO=∠AFP=90°,
∴△AOM∽△PAF,
∴$\frac{AM}{PF}=\frac{OM}{AF}$,
∴$\frac{2}{PF}=\frac{2\sqrt{3}}{2}$,
解得:PF=$\frac{2\sqrt{3}}{3}$,
∴EP=EF-PF=2$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴P2(4,$\frac{4\sqrt{3}}{3}$);
综上:P1(4,-$\frac{4\sqrt{3}}{3}$),P2(4,$\frac{4\sqrt{3}}{3}$).
点评 此题属于反比例函数综合题,考查了待定系数求函数解析式的知识以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,?ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP.
已知:如图,?ABCD中,CD=CB=2,∠C=60°,点E是CD边上自D向C的动点(点E运动到点C停止运动),连结AE,以AE为一边作等边△AEP,连结DP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
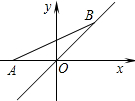 如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时点B的坐标为( )
如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时点B的坐标为( )| A. | (0,0) | B. | (-1,-1) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,-$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
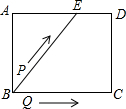 如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )| A. | 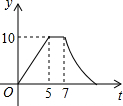 | B. | 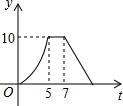 | C. |  | D. | 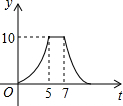 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com