
【题目】如果一个三角形有一边上的中线与这边的长相等,那么称这个三角形为“和谐三角形”.
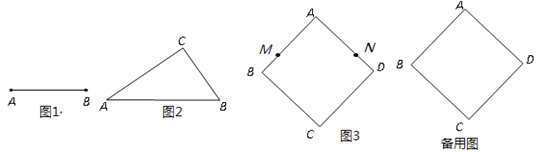
(1)请用直尺和圆规在图1中画一个以线段AB为一边的“和谐三角形”;
(2)如图2,在△ABC中,∠C=90°,AB=![]() ,BC=
,BC=![]() ,请你判断△ABC是否是“和谐三角形”?证明你的结论;
,请你判断△ABC是否是“和谐三角形”?证明你的结论;
(3)如图3,已知正方形ABCD的边长为1,动点M,N从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点M经过的路程为S,当△AMN为“和谐三角形”时,求S的值.
【答案】(1)作图见解析;
(2)△ABC是“和谐三角形”,理由见解析;
(3)当△AMN为“和谐三角形”时,S的值为![]() 或
或![]() .
.
【解析】解:(1)如图1,
作线段AB的中点O,
②以点O为圆心,AB长为半径画圆,
③在圆O上取一点C(点E、F除外),连接AC、BC.
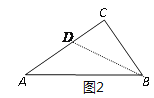 ∴△ABC是所求作的三角形.
∴△ABC是所求作的三角形.
(2)如图2,∠C=90°,AB=![]() ,BC=
,BC= ![]()
![]() ,CD=1,在Rt△BCD中,
,CD=1,在Rt△BCD中,
![]() ,∴中线BD=边AC,
,∴中线BD=边AC,
∴△ABC是“和谐三角形”;
(3)易知,点M在AB上时,△AMN是等腰直角三角形,不可能是“和谐三角形”,
当M在BC上时,连接AC交MN于点E,
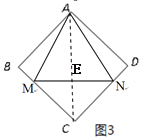 (Ⅰ)当底边MN的中线AE=MN时,如图,
(Ⅰ)当底边MN的中线AE=MN时,如图,
有题知AC=![]() ,MC=2-S,∴MN=
,MC=2-S,∴MN=![]() (2-s),CE=
(2-s),CE=![]() (2-S),
(2-S),
∵AE=MN,∴![]() ,S=
,S=![]() ,
,
(Ⅱ)当腰Am与它的中线NG相等,即AM=GN=AN时,
作NH⊥AM于H,如图
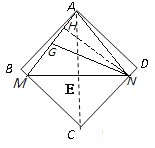 ∵NG=NA, NH⊥AM, ∴GH=AH=
∵NG=NA, NH⊥AM, ∴GH=AH=![]() GN=
GN= ![]() ,在Rt△NHA中,
,在Rt△NHA中,
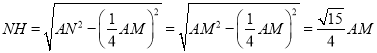
在Rt△NHM中,tan∠HMN=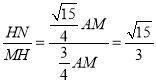 ;
;
在Rt△AME中, tan∠AME 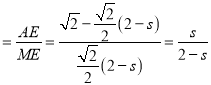 ;
; ![]() ;
;
![]() 。
。
综上,S=![]() 或
或![]() 时
时


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并在括号内填注理由:
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
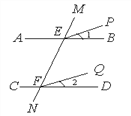
证明:∵AB∥CD,
∴∠MEB=∠MFD(_____________)
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥____.(_______________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若该二次函数的最小值为-4,求该二次函数解析式;
(2)当![]() 且
且![]() 时,函数值y的取值范围是-6≤y≤5-n,求n的值;
时,函数值y的取值范围是-6≤y≤5-n,求n的值;
(3)在(1)的条件下,将此二次函数平移,使平移后的图象经过(1,0).设平移后的图象对应的函数表达式为![]() ,当x<2时,y随x的增大而减小,求k的取值范围.
,当x<2时,y随x的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动近日推出“4G商旅套餐”,其中![]() 两种计费方法如下:
两种计费方法如下:
计费 | 月租费 | 国内主叫 | 国内主叫 | 备注 |
A | 58 |
| 150 | 全国范围内接听免费,含来电显示 |
B | 88 | 350 |
![]() 说明:
说明:![]() 指在国内任何地方拨打任何电话的资费;
指在国内任何地方拨打任何电话的资费;![]() 指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元
指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元![]() 月;若主叫时间为200分钟,则计费为
月;若主叫时间为200分钟,则计费为![]() 元
元![]()
![]() 在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
![]() 若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
![]() 经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com