
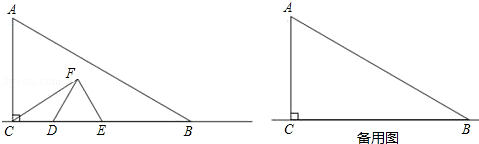
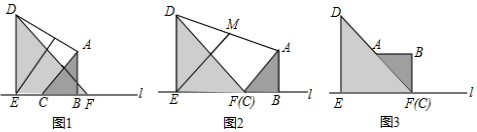
���� ��1���ٸ����˶���ʱ����ٶȣ������Ƴ�CD��CE�ij��ȣ�����Ƴ��߳�DE�ij��ȣ��ڸ��������Ƴ�CF�ij��ȣ�Ȼ��ͨ�����CEF=60�㣬��FCD=30���Ƴ�ֱ�������Σ������ݡ�CEF������ֵ�Ƴ�t��ֵ��
��2�����ȸ������⻭��ͼ�Σ�Ȼ������������۽�𣬢ٵ���A��DF���У�ͨ����֤��ACD�ա�AFD�������Ƴ���ʱBC���A�����ڵ�C��Ȼ��ͨ��ֱ��������������ǵĺ���ֵ�������Ƴ�t��ֵ��������A��CF���У����ݣ�1��������֤�Ľ��ۣ����ֱ��������������ǵĺ���ֵ�������Ƴ�t��ȡֵ��
��3��������������ۣ�����GE��ACʱ���ı���ACEGΪ���Σ�����FH��ͨ����ؽǵĶ�����ϵ�Ƴ�CF��FH��ͬһ��ֱ���ϣ�Ȼ��ͨ����֤��ACB�ס�HFE���Ƴ�$\frac{EF}{BC}$�������Ƴ�t��ֵ������AG��CEʱ���ı���ACEGΪ���Σ�����AF��FG�����ݶԳƵ����ʣ������Ƴ���AFM�ա�AGM�����á�FAM=��GAM����AFM=��AGM�����֪��AFE=90�㣬ͨ��A��F��E��ͬһ��ֱ���ϣ��Ƴ���ACE��Rt����������ֱ��������������ǵĺ���ֵ�����Ƴ�t��ֵ��
��� �⣺��1���١ߵ�D��E�ӵ�Cͬʱ�������ֱ���1cm/s��2cm/s���ٶ��ƶ���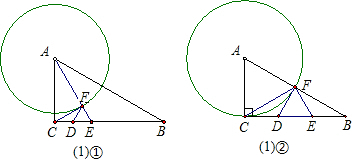
���D��E�˶���ʱ��Ϊt�룬
��CD=1t=t��CE=2t��
��DE=CE-CD=2t-t=t��
�ߵȱߡ�DEF��
��DE=DF=EF=t�����߳�Ϊt��
�ڵ�F��AB��ʱ��
��DE=t��
��CD=DE=EF=DF=t��
�ߵȱߡ�DEF��
���FDE=60�㣬
���FCD=30�㣬
���ACF=60�㣬
�ߡ�A=60�㣬��B=30�㣬
�൱F��AB��CF=AF=BF��
��BC=6��
��AB=4$\sqrt{3}$��AC=2$\sqrt{3}$��
��CF=2$\sqrt{3}$��
�ߡ�CEF=60�㣬
��CF��EF��
��sin60��=$\frac{\sqrt{3}}{2}$=$\frac{CF}{CE}$��
��CE=2t��
��$\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{2t}$��
��t=2��
��2���ٵ���A��DF���У�����AD��
�ߡ�A��DF���У�
��AB��DF��
�֡�AC��BC��
���ACD=��AFD=90�㣬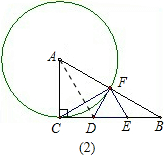
�֡�AD=AD��AC=AF��
���ACD�ա�AFD��HL����
��AF=AC��
��BC���A�����ڵ�C��
��AC=2$\sqrt{3}$����FDB=60�㣬
���ADC=60�㣬
��CD=t��
��tan60��=$\frac{AC}{CD}=\sqrt{3}$��
��t=2��
������A��CF����
��CF��AF��
��AC=2$\sqrt{3}$����ACF=60�㣬
��cos60��=$\frac{CF}{AC}=\frac{1}{2}$��
��CF=$\sqrt{3}$��
�ߡ�FCE=30�㣬��FEC=60�㣬
��EF��CF��
��cos30��=$\frac{CF}{CE}=\frac{\sqrt{3}}{2}$��
��CE=2t��
��$\frac{\sqrt{3}}{2t}=\frac{\sqrt{3}}{2}$��
��t=1��
��3����t=1.5��t=1ʱ��ʹ����A��C��E��GΪ������ı���Ϊ���Σ�
����ͼ����GE��ACʱ���ı���ACEGΪ���Σ�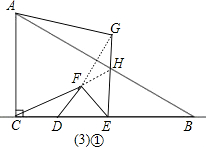
����FH��
��AC��BC��
��GE��BC��
�ߡ�B=30�㣬
���G=30�㣬
��F��G�������AB�ɶԳƵ㣬
���GFH=30�㣬
�ߡ�FEC=60�㣬
���FEG=30�㣬
���GFE=120�㣬
���HFE=90�㣬
�ߡ�CFD=60�㣬��DEF=30�㣬
���CFH=180�㣬��CF��FH��ͬһ��ֱ���ϣ�
�ߡ�ACF=��A=60�㣬��FCB=��B=30�㣬
��CH=AH=HB��
��AB=4$\sqrt{3}$��
��CH=AH=HB=2$\sqrt{3}$��
��HE=$\sqrt{3}$��
�ߡ�FEH=��B=30�㣬��ACB=��HFE=90�㣬
���ACB�ס�HFE��
��$\frac{EF}{BC}=\frac{HE}{AB}$��
��AB=4$\sqrt{3}$��BC=6��
��HE=$\sqrt{3}$��EF=t��
��t=1.5��
����AG��CEʱ���ı���ACEGΪ���Σ�
����AF��FG������AB����M�㣬
��G��F�������AB�Գƣ�
��AF=AG��FM=GM��AB��FG��
���AFM�ա�AGM��
���FAM=��GAM����AFM=��AGM��
��AG��BC��
���B=��GAM=30�㣬
���FAM=30�㣬
���AFM=60�㣬
�ߡ�FED=60�㣬��B=30�㣬
���FEB=120�㣬
�����ı���MFEB�У���FMB=90�㣬
���FEB=120�㣬
�ߡ�CFE=90�㣬��AFM=60�㣬
���AFE=180�㣬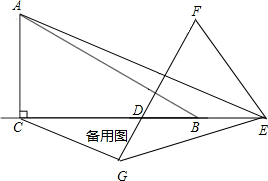
��A��F��E��ͬһ��ֱ���ϣ�
�ߡ�AFC=90�㣬
���ACE��ֱ�������Σ�
�ߡ�CEF=60�㣬
��tan60��=$\frac{AC}{EC}=\sqrt{3}$����$\frac{2\sqrt{3}}{2t}=\sqrt{3}$��
��t=1��
���籸��ͼ��
��t=$\frac{3+\sqrt{21}}{2}$ʱ��ʹ����A��C��E��GΪ������ı���Ϊ���Σ�
���Ͽɵõ�t=1.5��t=1��t=$\frac{3+\sqrt{21}}{2}$ʱ��ʹ����A��C��E��GΪ������ı���Ϊ���Σ�
���� ������Ҫ�������ߵ����ʡ�ȫ�������ε��ж������ʡ���ֱ�������Ρ��ȱ������ε����ʣ��ؼ�������ȷ���������ߣ�����ؼ��㣬����������صĶ��������ʣ�


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
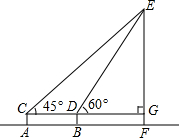 ��ͼ��Ϊ�˲�������ĸ߶ȣ�СӨ�������ƵIJ���ǣ���C��������E������Ϊ45�㣬��D��������E������Ϊ60�㣬��֪�����AC�ĸ�Ϊ1.6�ף�CD�ij�Ϊ6�ף�CD���ڵ�ˮƽ��CG��EF�ڵ�G������EF�ĸ�Ϊ��10.6+3$\sqrt{3}$���ף�������ô����ŵ�ʽ�ӱ�ʾ��
��ͼ��Ϊ�˲�������ĸ߶ȣ�СӨ�������ƵIJ���ǣ���C��������E������Ϊ45�㣬��D��������E������Ϊ60�㣬��֪�����AC�ĸ�Ϊ1.6�ף�CD�ij�Ϊ6�ף�CD���ڵ�ˮƽ��CG��EF�ڵ�G������EF�ĸ�Ϊ��10.6+3$\sqrt{3}$���ף�������ô����ŵ�ʽ�ӱ�ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
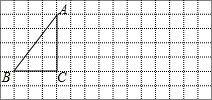 ��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
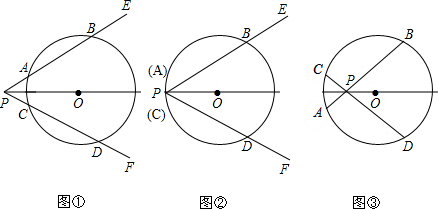
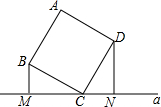 ��ͼ��������ABCD�Ķ���C��ֱ��a�ϣ���BM��ֱ��a��M��DN��ֱ��a��N
��ͼ��������ABCD�Ķ���C��ֱ��a�ϣ���BM��ֱ��a��M��DN��ֱ��a��N �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com