解:(1)抛物线解析式y=ax
2+bx+3经过A(-3,0),B(-1,0)两点,
∴
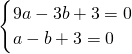
,
解得
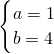
,
∴抛物线的解析式为y=x
2+4x+3.
(2)由(1)配方得y=(x+2)
2-1,
∴抛物线的顶点坐标为M(-2,-1),
∴直线OD的解析式为y=

x,
于是可设平移后的抛物线的顶点坐标为(h,

h),
∴平移后的抛物线的解析式为y=(x-h)
2+

h,
当抛物线经过点C时,∵C(0,9),
∴h
2+

h=9.
解得h=
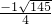
,
∴当
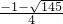
≤h<
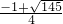
时,平移后的抛物线与射线CD只有一个公共点;
当抛物线与直线CD只有一个公共点时,
由方程组
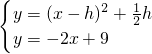
,
得x
2+(-2h+2)x+h
2+

h-9=0,
∴△=(-2h+2)
2-4(h
2+

h-9)=0,
解得h=4,
此时抛物线y=(x-4)
2+2与直线CD唯一的公共点为(3,3),点(3,3)在射线CD上,符合题意.
∴平移后抛物线与射线CD只有一个公共点时,顶点横坐标的取值范围是
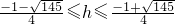
或h=4.
(3)平移后,当E(-1,0)、F(5,0)时,抛物线的解析式为:
y=(x+1)(x-5),即y=x
2-4x-5.
当x=0时,y=-5.
∴N(0,-5).
∴OF=ON=5,
假设存在点G,使△GFN中FN边上的高为7

,
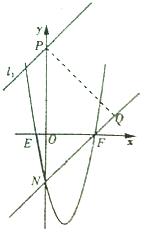
∴G点应在与直线FN平行,且相距7

的两条平行线l
1(如图所示)和l
2(在直线FN下方且平行于直线FN)上.
由平行的性质可以知道l1和l2与y轴的交点到直线FN的距离也为7

,如图,设l1与y轴交于点P,过点P作PQ⊥FN,垂足为Q,
∵OF=ON,
∴∠ONF=OFN=45°.
在Rt△PQN中,PQ=7

,∠PNQ=∠ONF=45°,
由勾股定理,得PN=

PQ=14.
∴直线l1与y轴的交点坐标为P(0,9).
同理可得:直线l2与y轴的交点坐标为R(0,-19).
∵OF=ON=5,
∴F(5,0),N(0,-5),
∴容易求得直线FN的解析式为:y=x-5.
∴直线l
1、l
2的解析式分别为l
1:y=x+9;l
2:y=x-19.
根据题意,列方程组:①
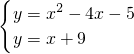
,
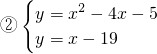
,
由①,得x
2-5x-14=0,解得x
1=7,x
2=-2
∴
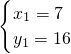
,
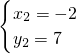
.
∴G
1(7,16),G
2(-2,7).
由②,得x
2-5x+14=0.
∵△=(-5)2-4×1×14<0,此方程无实数根.
∴在抛物线上存在点G,使△GFN中FN边上的高为7

.点G的坐标为:
G
1(7,16),G
2(-2,7).
分析:(1)直接用待定系数法就可以求出抛物线的解析式;
(2)由(1)的解析式求出抛物线的顶点坐标,根据抛物线的顶点坐标求出直线OD的解析式,设平移后的抛物线的顶点坐标为(h,

h),就可以表示出平移后的解析式,当抛物线经过点C时就可以求出h值,抛物线与直线CD只有一个公共点时可以得出
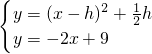
,得x
2+(-2h+2)x+h
2+

h-9=0,从而得出△=(-2h+2)
2-4(h
2+

h-9)=0求出h=4,从而得出结论;
(3)根据条件平移后求出抛物线的解析,求出直线FN的解析式,从而求出l
1,l
2的解析式,利用直线的解析式与抛物线的解析式构建方程组就可以求出其交点坐标就实G点的坐标.
点评:本题是一道二次函数的综合试题,考查了待定系数法求抛物线的解析式,二次函数图象与几何变换,勾股定理的运用及方程组与交点坐标的运用.

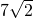 ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.
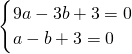 ,
,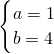 ,
, x,
x, h),
h), h,
h, h=9.
h=9.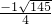 ,
,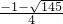 ≤h<
≤h<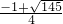 时,平移后的抛物线与射线CD只有一个公共点;
时,平移后的抛物线与射线CD只有一个公共点;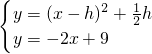 ,
, h-9=0,
h-9=0, h-9)=0,
h-9)=0,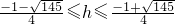 或h=4.
或h=4. ,
, 的两条平行线l1(如图所示)和l2(在直线FN下方且平行于直线FN)上.
的两条平行线l1(如图所示)和l2(在直线FN下方且平行于直线FN)上. ,如图,设l1与y轴交于点P,过点P作PQ⊥FN,垂足为Q,
,如图,设l1与y轴交于点P,过点P作PQ⊥FN,垂足为Q, ,∠PNQ=∠ONF=45°,
,∠PNQ=∠ONF=45°, PQ=14.
PQ=14.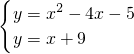 ,
,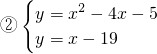 ,
,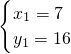 ,
,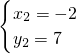 .
. .点G的坐标为:
.点G的坐标为:
 h),就可以表示出平移后的解析式,当抛物线经过点C时就可以求出h值,抛物线与直线CD只有一个公共点时可以得出
h),就可以表示出平移后的解析式,当抛物线经过点C时就可以求出h值,抛物线与直线CD只有一个公共点时可以得出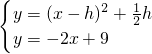 ,得x2+(-2h+2)x+h2+
,得x2+(-2h+2)x+h2+ h-9=0,从而得出△=(-2h+2)2-4(h2+
h-9=0,从而得出△=(-2h+2)2-4(h2+ h-9)=0求出h=4,从而得出结论;
h-9)=0求出h=4,从而得出结论;

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案

 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.