
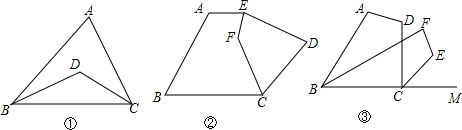
分析 (1)首先根据三角形的内角和定理,求出∠ABC、∠ACB的度数和是多少;然后根据∠ABC、∠ACB的平分线交于点D,求出∠DBC、∠DCB的度数和是多少;最后在△BCD中,根据三角形的内角和定理,用180°减去∠DBC、∠DCB的度数和,求出∠BDC的度数是多少即可.
(2)首先根据AE∥BC,可得∠A+∠B=180°,再用五边形的内角和减去180°,求出∠AED、∠EDC、∠BCD的度数和是多少;然后根据∠EDC=70°,求出∠AED、∠EDC的度数和是多少;最后根据EF平分∠AED,CF平分∠BCD,求出∠FED、∠FCD的度数和是多少;再用四边形CDEF的内角和减去∠FED、∠FCD、∠EDC的度数和,求出∠EFC的度数是多少即可.
(3)首先根据∠A+∠D=210°,求出∠ABF、∠CBF、∠BCD的度数和是150°;再根据BF平分∠ABC,判断出2∠CBF+∠BCD=150°…①;然后判断出∠BCD+2∠DCE=180°…②,由①②,可得2∠CBF+2∠BCD+2∠DCE=150°+180°=330°,据此求出∠CBF+∠BCD+∠DCE=330°÷2=165°;最后用360°减去∠CBF、∠BCD、∠DCE、∠E的度数和,求出∠F的度数是多少即可.
解答 解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠ABC、∠ACB的平分线交于点D,
∴∠ABD=∠DBC,∠DCB=∠ACD,
∴∠DBC+∠DCB=120°÷2=60°,
∴∠BDC=180°-60°=120°.
(2)∵AE∥BC,
∴∠A+∠B=180°,
∵五边形ABCDE的内角和是:
180°×(5-2)=180°×3=540°,
∴∠AED+∠EDC+∠BCD=540°-180°=360°,
∵∠EDC=70°,
∴∠AED+∠BCD=360°-70°=290°,
∵EF平分∠AED,CF平分∠BCD,
∴∠FED+∠FCD=290°÷2=145°,
∴∠EFC=360°-(∠FED+∠FCD+∠EDC)
=360°-(145°+70°)
=360°-215°
=145°
(3)四边形的内角和是:
180°×(4-2)=180°×2=360°,
∵∠A+∠D=210°,
∴∠ABF+∠CBF+∠BCD=360°-210°=150°,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴2∠CBF+∠BCD=150°…①;
∵CE平分∠DCM,
∴∠DCE=∠MCE,
又∵∠BCD+∠DCE+∠MCE=180°,
∴∠BCD+2∠DCE=180°…②,
由①②,可得
2∠CBF+2∠BCD+2∠DCE=150°+180°=330°,
∴∠CBF+∠BCD+∠DCE=330°÷2=165°,
∴∠F=360°-(∠CBF+∠BCD+∠DCE)-∠E
=360°-165°-110°
=85°
故答案为:120°、145°、∠F=85°.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的角平分线把这个角分成两个大小相等的角.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
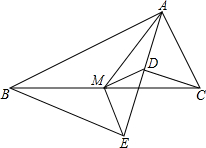 如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
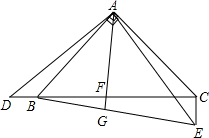 在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.
在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com