
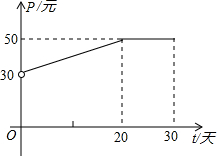
 根据市场调查,某种新产品投放市场30天内,每件产品的销售价格
根据市场调查,某种新产品投放市场30天内,每件产品的销售价格| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
|
|
|
|


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
 已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF
已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF| CE |
| CD |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
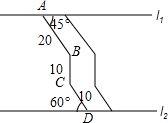 如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.
如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com