
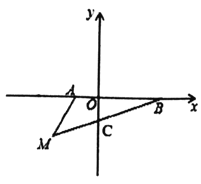
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)填空:![]() _______,
_______,![]() ________;
________;
(2)若在第三象限内有一点![]() ,用含
,用含![]() 的式子表示
的式子表示![]() 的面积;
的面积;
(3)在(2)条件下,当![]() 时,点
时,点![]() 是坐标轴上的动点,当满足
是坐标轴上的动点,当满足![]() 的面积是
的面积是![]() 的面积的2倍时,求点
的面积的2倍时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2) ![]() ;(3) (
;(3) (![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)利用非负数的性质求得![]() 、
、![]() 的值,即可得出答案;
的值,即可得出答案;
(2)过M作ME⊥![]() 轴于E,根据三角形的面积公式即可得到结果;
轴于E,根据三角形的面积公式即可得到结果;
(3)分类讨论,P点可以在x轴上,也可以在y轴上,根据点的坐标特征以及面积公式求解即可.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
(2)如图1所示,过M作CE⊥![]() 轴于E,
轴于E,

∵![]() ,
,![]() ,
,
∴A(-1,0),B(3,0),
∴OA=1,OB=3,
∴AB=4,
∵在第三象限内有一点M(-2,m),
∴ME![]() ,
,
∴S△ABM=![]() AB×ME=
AB×ME=![]() ×4×(
×4×(![]() )=
)=![]() ;
;
(2)当![]() 时,点M的坐标为(
时,点M的坐标为(![]() ,
,![]() ), S△ABM=
), S△ABM=![]() ,
,
∴![]() ,
,
设直线BM交![]() 轴于C点,
轴于C点,
①当点P在![]() 轴上时,如图:
轴上时,如图:

∵![]()
解得:PC=![]() ,
,
设直线BM的解析式为![]() ,
,
把点M(![]() ,
,![]() ), B(3,0)代入得:
), B(3,0)代入得: ,
,
解得: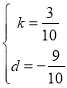 ,
,
∴直线BM的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴点C的坐标为(![]() ,
,![]() ),
),
∴OC=![]() ,
,
当点P在点C的下方时,点P的坐标为(![]() ,
,![]() ),即P(
),即P(![]() ,
,![]() ),
),
当点P在点C的上方时,点P的坐标为(![]() ,
,![]() ),即
),即![]() (
(![]() ,
,![]() ),
),
②当P在![]() 轴上且在点A的左侧时,设P点的坐标为(
轴上且在点A的左侧时,设P点的坐标为(![]() ,0),如图:
,0),如图:

∵![]() ,
,
∴PB=2AB,
∵B(3,0),AB=4,
∴![]() ,
,
∴![]() ,
,
∴P点的坐标为(![]() ,0),
,0),
当P在![]() 轴上且在点B的D右侧时,设P点的坐标为(
轴上且在点B的D右侧时,设P点的坐标为(![]() ,0),如图:
,0),如图:
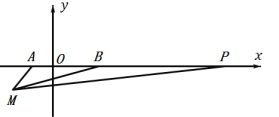
同理,PB=2AB,
∵B(3,0),AB=4,
∴![]() ,
,
∴![]() ,
,
∴P点的坐标为(![]() ,0),
,0),
综合上述:P点的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
(1)等腰直角三角形是不是“少见的三角形”?
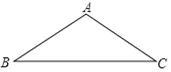
(2)已知如图所示的钝角三角形是一个“少见的三角形”,请你画出分割线的大致位置,并求出顶角的度数;
(3)锐角三角形中有没有“少见的三角形”?如果没有,请说明理由;如果有,请画出图形并求出顶角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查方式的是( )
A.对同批次![]() 灯泡的使用寿命的调查
灯泡的使用寿命的调查
B.对乘坐飞机的旅客是否携带违禁物品的调查
C.对一个社区每天丢弃塑料袋数量的调查
D.对中央电视台“战疫情”栏目收视率的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
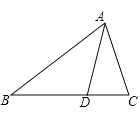
【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如图: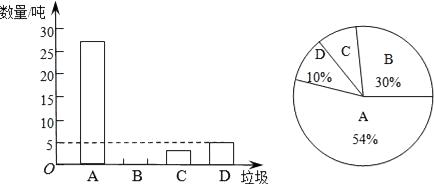
(注:A为可回收物,B为厨余垃圾,C为有害垃圾,D为其他垃圾)
根据图表解答下列问题:
(1)在抽样数据中,产生的有害垃圾共多少吨?
(2)请将条形统计图补充完整;
(3)调查发现,在可回收物中塑料类垃圾占 ![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.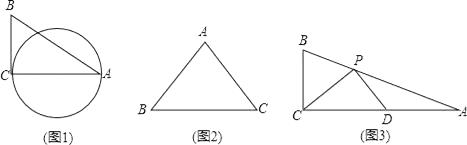
(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组数据:98,99,99,100和98.5,99,99,99.5,则关于以下统计量说法不正确的是( )
A. 平均数相等
B. 中位数相等
C. 众数相等
D. 方差相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图:
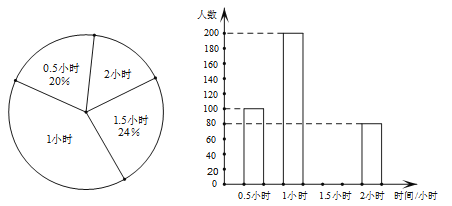
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com