
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P��a��b���͵�Q��a��b'�����������¶��壺
��b'=![]() ����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
��1���ٵ㣨��![]() ��1�����ޱ����������� ����
��1�����ޱ����������� ����
���ڵ�A����1��2����B����2����1������һ�����Ǻ���y=![]() ͼ����ijһ��������㣬��������� ����
ͼ����ijһ��������㣬��������� ����
��2������P�ں���y=��x+3��ͼ���ϣ�����2��x��6ʱ�������ޱ��Q��������b'��ȡֵ��Χ��
��3������P�ڹ���x�Ķ��κ���y=x2��2tx+t2+t��ͼ���ϣ����ޱ��Q��������b'��ȡֵ��Χ��b'��m��b'��n������m��n����s=m��n����s����t�ĺ�������ʽ��s��ȡֵ��Χ��
���𰸡���1��������![]() ����1������A����2������2��x��6ʱ����5��b���2����3��s����t�ĺ�������ʽΪs=t2+1��t��1����s��ȡֵ��Χ��s��2��
����1������A����2������2��x��6ʱ����5��b���2����3��s����t�ĺ�������ʽΪs=t2+1��t��1����s��ȡֵ��Χ��s��2��
��������
��1����ֱ�Ӹ����ޱ��Ķ���ֱ�ӵó��𰸣�
�ڵ㣨-1��-2���ڷ���������ͼ���ϣ��㣨-1��-2�����ޱ��Ϊ��-1��2�����ݴ˵õ��𰸣�
��2�����������֪y=-x+3��x��-2��ͼ���ϵĵ�P���ޱ��Q���ں���y=![]() ��ͼ���ϣ����ͼ�ɵõ��𰸣�
��ͼ���ϣ����ͼ�ɵõ��𰸣�
��3���������y=x2-2tx+t2+t�������꣬���t��1�Ĺ�ϵȷ��y����ֵ��������m��n��ʾ��s������t��ȡֵ��Χ���s��ȡֵ��Χ��
��1���ٸ����ޱ��Ķ����֪��㣨��![]() ��1�����ޱ�������Ϊ����
��1�����ޱ�������Ϊ����![]() ����1����
����1����
������1����2���ޱ��Ϊ����1��2������������ǵ�A��
��2�������⣬y=��x+3��x�ݩ�2��ͼ���ϵĵ�P���ޱ��Q���ں���y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��x=��2ʱ��y=��2��3=��5��
��x=1ʱ��y=��1+3=2��
��x=6ʱ��y=��6+3=��3��
�൱��2��x��6ʱ����5��b���2��
��3����y=x2��2tx+t2+t=��x��t��2+t��
�ඥ������Ϊ��t��t����
��t��1��b����ȡֵ��Χ��b���m��b�䣼n�������ⲻ����
��t��1����x��1ʱ��y����СֵΪt����m=t��
��x��1ʱ��y��ֵС�ک�[��1��t��2+t]����n=��[��1��t��2+t]��
��s=m��n=t+��1��t��2+t=t2+1��
��s����t�ĺ�������ʽΪs=t2+1��t��1����
��t=1ʱ��sȡ��Сֵ2��
��s��ȡֵ��Χ��s��2��


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
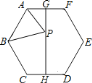
����Ŀ����ͼ����֪��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ��
��![]() ����
����![]() ����СֵΪ�� ��
����СֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
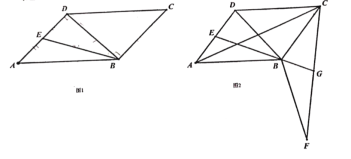
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��� A��B������ֱ�Ϊ��0��3������1��0������ABC�ǵ���ֱ�������Σ���ABC��90�㣮
��1��ͼ1�У���C������Ϊ ��
(2)��ͼ2����D������Ϊ��0��1������E������CD�ϣ�����B ��BF��BE��y���ڵ�F��
�ٵ���EΪ�߶�CD���е�ʱ�����F�����ꣻ
�ڵ���E�ڵڶ�����ʱ����ֱ��д��F��������y��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
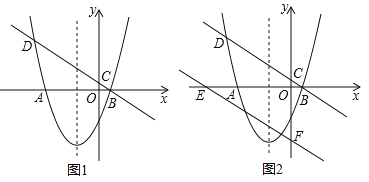
����Ŀ����ͼ1��������y=ax2+2x+c��x�ύ��A����4��0����B��1��0�����㣬����B��ֱ��y=kx+![]() �ֱ���y�ἰ�����߽��ڵ�C��D��
�ֱ���y�ἰ�����߽��ڵ�C��D��
��1����ֱ�ߺ������ߵı���ʽ��
��2������P�ӵ�O��������x��ĸ���������ÿ��1����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����PDCΪֱ�������Σ���ֱ��д����������������t��ֵ��
��3����ͼ2����ֱ��BD��y������ƽ��4����λ����x�ᣬy��ֱ���E��F���㣬�������ߵĶԳ������Ƿ���ڵ�M����ֱ��EF���Ƿ���ڵ�N��ʹDM+MN��ֵ��С�������ڣ��������Сֵ����M��N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����κ�����������������
�ٺ���ͼ����x��Ľ�������ֱ�ΪA��1��0����B��x2��y2������B�ڵ�A���Ҳࣩ��
�ڶԳ�����x=3��
�۸ú�������Сֵ�ǩ�2��
��1�������������Ϣ������κ�������ʽ��
��2�����ú���ͼ��x��x2�IJ���ͼ�����·�����ԭͼ��δ���۵IJ������ͼ����G����ƽ����x���ֱ����ͼ����G���ཻ�ڵ�C��x3��y3����D��x4��y4����E��x5��y5����x3��x4��x5������ϻ����ĺ���ͼ����x3+x4+x5��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������з�����ز����й�������־��Ʒ�����£���ֵ����������������ij�̼ҿ��̻�����һ����4800Ԫ����һ�������ȣ��������ã����ǵڶ�������12000Ԫ����һ�������ȣ�����ʱ���۱ȵ�һ������2Ԫ��������������ǡ���ǵ�һ�ι�������������.
��1�����һ�ι��������ȵĽ���.
��2��ʵ�������У������ۼ۾���ͬ�������۹����У�������������ѡ��Ʒ�½�����һ�������ȵ����100ǧ�˰����۳����ڶ��������ȵ����800ǧ�˾����۳��������������������ȵĻ���������9400Ԫ�����ۼ�����Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ���ı���![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() �ߵ��е㣬����
�ߵ��е㣬����![]() ��
��
��1����ͼ1����![]() ��
��![]() ����ƽ���ı���
����ƽ���ı���![]() �������
�������
��2����ͼ2������![]() ����
����![]() ��
��![]() ���۵õ�
���۵õ�![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͨѶ��˾�Ƴ�����������ͨѶ�շѷ�ʽ���û�ѡ������һ��������ѣ���һ��������ѣ��������շѷ�ʽ��ͨѶʱ��x(��)�����y(Ԫ)֮��ĺ�����ϵ��ͼ��ʾ��
(1)��������շѷ�ʽ��________(����������������)���������________Ԫ��
(2)�ֱ���������������շѷ�ʽ��y���Ա���x֮��ĺ�������ʽ��
(3)��������û�ͨѶʱ��Ķ��٣���������ʵ�ݵ�ѡ���飮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ���������ܱ�ʾ����������ż����ƽ�����ô�����������Ϊ�����������磺![]() ��
��![]() ��
��![]() �����4,12,20��������������������.
�����4,12,20��������������������.
��1��400��2020���������ǡ���������Ϊʲô��
��2������������ż��Ϊ![]() ��
��![]() ������
������![]() ȡ����������������������ż������ġ���������4�ı�����Ϊʲô��
ȡ����������������������ż������ġ���������4�ı�����Ϊʲô��
��3�������50��101֮�����С�������֮��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com