
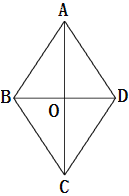
【题目】如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.
(1)求菱形ABCD的周长;
(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;
(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.
【答案】(1)200;(2)480;(3)2,![]() .
.
【解析】
试题分析:本题考查了相似三角形的判定与性质、菱形、等腰三角形、中垂线、勾股定理、解直角三角形、二次函数极值等知识点,涉及考点较多,有一定的难度.第(2)问中,动点M在线段AO和OD上运动时,是两种不同的情形,需要分类讨论;第(3)问中,满足条件的点有2个,注意不要漏解.
(1)根据勾股定理及菱形的性质,求出菱形的周长;
(2)在动点M、N运动过程中:①当0<t≤40时,如答图1所示,②当40<t≤50时,如答图2所示.分别求出S的关系式,然后利用二次函数的性质求出最大值;
(3)如答图4所示,作ON的垂直平分线,交EF于点I,连接OI,IN.过点N作NG⊥OD,NH⊥EF,垂足分别为G,H.易得△DNG∽△DAO,由EF垂直平分OD,得到OE=ED=15,EG=NH=3,再设OI=R,EI=x,根据勾股定理,在Rt△OEI和Rt△NIH中,得到关于R和x的 方程组,解得R和x的值,把二者相加就是点P到OD的距离,即PE=PI+IE=R+x,又根据对称性可得,在BD下方还存在一个点P′也满足条件,故存在两个点P,到OD的距离也相同,从而问题解决.
试题解析:(1)如图①)在菱形ABCD中,OA=![]() AC=40, OD=
AC=40, OD=![]() BD=30,
BD=30,
∵AC⊥BD,
∴AD=![]() =50,
=50,
∴菱形ABCD的周长为200;
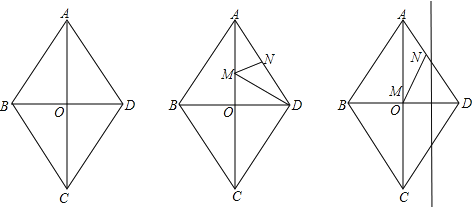
(2)(如图②)过点M作MH⊥AD于点H.
① (如图②甲)①当0<t≤40时,
∵sin∠OAD=![]() =
=![]() =
=![]() ,
,
∴MH=![]() t,
t,
∴S=![]() DN·MH=
DN·MH=![]() t2.
t2.
②(如图②乙)当40<t≤50时,
∴MD=80-t,
∵sin∠ADO=![]() -
-![]() ,
,
∴MH=![]() (70-t),
(70-t),
∴S=![]() DN·MH,
DN·MH,
=-![]() t2+28t
t2+28t
=-![]() (t-35)2+490.
(t-35)2+490.
∴S=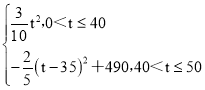 ,
,
当0<t≤40时,S随t的增大而增大,当t=40时,最大值为480.
当40<t≤50时,S随t的增大而增大,当t=40时,最大值为480.
综上所述,S的最大值为480;

(3)存在2个点P,使得∠DPO=∠DON.
(如图④)作ON的垂直平分线,交EF于点I,连接OI,IN.
过点N作NG⊥OD,NH⊥EF,垂足分别为G,H.
当t=30时,DN=OD=30,易知△DNG∽△DAO,
∴NG=24,DG=18.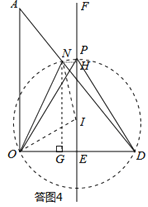
∵EF垂直平分OD,
∴OE=ED=15,EG=NH=3,
设OI=R,EI=x,则
在Rt△OEI中,有R2=152+x2……①,
在Rt△NIH中,有R2=32+(24-x)2……②,
由①,②可得: ,
,
∴PE=PI+IE=![]() .
.
根据对称性可得,在BD下方还存在一个点P′也满足条件,
∴存在两个点P,到OD的距离都是![]() .
.



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】算24点游戏是一种使用扑克牌来进行的益智类游戏,游戏内容是:从一副扑克牌中抽去大小王剩下52张,任意抽取4张牌,把牌面上的数运用你所学过的加、减、乘、除、乘方运算得出24.每张牌都必须使用一次,但不能重复使用.
(1)如图1,在玩“24点”游戏时,小明抽到以下4张牌:

请你帮他写出运算结果为24的算式:(写出2个); 、 ;
(2)如图2,如果![]() 、
、![]() 表示正,
表示正,![]() .
.![]() 表示负,J表示11点,Q表示12点.请你用下列4张牌表示的数写出运算结果为24的算式(写出1个): .
表示负,J表示11点,Q表示12点.请你用下列4张牌表示的数写出运算结果为24的算式(写出1个): .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙在400米的直线跑道上从同一地点同向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,跑步过程中两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
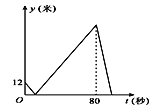
A. 乙的速度是4米/秒
B. 离开起点后,甲、乙两人第一次相遇时,距离起点12米
C. 甲从起点到终点共用时83秒
D. 乙到达终点时,甲、乙两人相距68米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆统景温泉风景区被喻为“巴渝十二景”.为丰富旅游配套资源,镇政府决定大力发动农户扩大柑橘和蔬菜种植面积,并取得了较好的经济效益.今年该镇柑橘和蔬菜的收成比去年增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到了420吨.
(1)统景镇去年柑橘和蔬菜的收成各是多少吨?
(2)由于今年大丰收,镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜一次性运去参加渝洽会.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘5吨和蔬菜6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
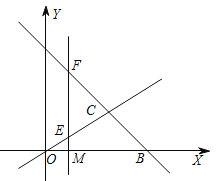
【题目】如图,直线OC,BC的函数关系式分别是y1=![]() x和y2=-x+6,两直线的交点为C.
x和y2=-x+6,两直线的交点为C.
(1)求点C的坐标,并直接写出y1>y2时x的范围;
(2)在直线y1上找点D,使△DCB的面积是△COB的一半,求点D的坐标;
(3)点M(t,0)是![]() 轴上的任意一点,过点M作直线l⊥
轴上的任意一点,过点M作直线l⊥![]() 轴,分别交直线y1、 y2于点E、F,当E、F两点间的距离不超过4时,求t的取值范围.
轴,分别交直线y1、 y2于点E、F,当E、F两点间的距离不超过4时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
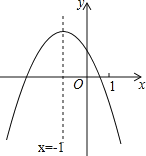
①b2﹣4ac>0;
②4a+c>2b;
③(a+c)2>b2;
④x(ax+b)≤a﹣b.
其中正确结论的是 .(请把正确结论的序号都填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com