
【题目】如图,矩形ABCD中,AB=4,BC=3,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
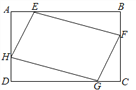
A. 7 B. 10 C. 14 D. 15
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,第2018次输出的结果为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)A景区与C景区之间的距离是多少?
(3)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充足电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,D的坐标为(1,0),(3,0),(0,1),点C在第四象限,∠ACB=90°,AC=BC.若△ABC与△A'B'C'关于点D成中心对称,则点C'的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+ ![]() x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).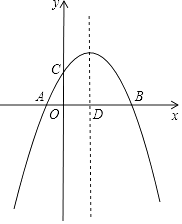
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:+(-2),0,﹣0.314,![]() (两个1间的0的个数依次多1个)﹣(﹣11),
(两个1间的0的个数依次多1个)﹣(﹣11),![]() ,
,![]() ,
,![]() ,
,![]()
正有理数集合:{ …},
无理数集合: { …},
整数集合: { …},
分数集合: { …}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com