

|
思路解析:建立适当的坐标系可以简化解题步骤.先建立如图26.3-13.2的坐标系,根据已知条件求出抛物线的解析式,再求抛物线上纵坐标为2.8的点之间的距离,若这个距离大于汽车装货宽度,就可判断汽车能顺利通过大门.
解:如图,以大门地面的中点为原点,大门地面为x轴,建立直角坐标系.根据对称性,设二次函数关系式为y=a(x+2)(x-2)(a≠0), 由已知,这个函数的图象过(0,4.4),可以得到4.4=a(0+2)(0-2). 解得a=-1.1. 所以所求二次函数的关系式是y=-1.1x2+4.4. 当y=2.8时,有-1.1x2+4.4=2.8. 解方程,得x1≈1.21,x2≈-1.21. 因为2×1.21>2.4, 所以,汽车能顺利通过大门. |


科目:初中数学 来源: 题型:
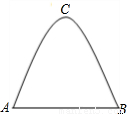
 某工厂大门是一抛物线水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高为4.4米,
某工厂大门是一抛物线水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高为4.4米,查看答案和解析>>
科目:初中数学 来源:2010-2011学年新人教版九年级(上)第三次月考数学试卷(26-27章)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com