
| ΒΎ1Ηω | ΒΎ2Ηω | ΒΎ3Ηω | ΒΎ4Ηω | Γ≠ | ΒΎnΗω | |
| Βς’ϊ«ΑΒΞΦέx Θ®‘ΣΘ© | x1 | x2=6 | x3=72 | x4 | Γ≠ | xn |
| Βς’ϊΚσΒΞΦέy Θ®‘ΣΘ© | y1 | y2=4 | y3=59 | y4 | Γ≠ | yn |
Ζ÷Έω Θ®1Θ©…ηy=kx+bΘ§Α―Θ®6Θ§4Θ©Θ§Θ®72.59Θ©¥ζ»κΒΟΒΫ$\left\{\begin{array}{l}{6k+b=4}\\{72k+b=59}\end{array}\right.$Θ§ΫβΖΫ≥ΧΉιΦ¥Ω…Θ°
Θ®2Θ©άϊ”ΟΘ®1Θ©ΒΡΙΊœΒ Ϋ«σ≥ωyΘ§«σ≤νΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®3Θ©≤¬œκΘΚ$\overline y$=$\frac{5}{6}$$\overline x$-1Θ§ΗυΨίΤΫΨυΒΞΦέΒΡΕ®“εΘ§Ν–≥ω ΫΉ”ΦΤΥψΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚΘ®1Θ©…ηy=kx+bΘ§Α―Θ®6Θ§4Θ©Θ§Θ®72.59Θ©¥ζ»κΒΟΒΫ$\left\{\begin{array}{l}{6k+b=4}\\{72k+b=59}\end{array}\right.$Θ§
ΫβΒΟ$\left\{\begin{array}{l}{k=\frac{5}{6}}\\{b=-1}\end{array}\right.$
Γύy=$\frac{5}{6}$x-1Θ®xΘΨ$\frac{18}{5}$Θ©Θ°
Θ®2Θ©Β±x=108 ±Θ§y=89Θ§
108-89=19Θ§
ΓύΙΥΩΆΙΚ¬ρ’βΗωΆφΨΏ ΓΝΥ19‘ΣΘ°
Θ®3Θ©≤¬œκΘΚ$\overline y$=$\frac{5}{6}$$\overline x$-1
÷ΛΟςΘΚy1=$\frac{5}{6}$x1-1Θ§y2=$\frac{5}{6}$x2-1Θ§Γ≠Θ§yn=$\frac{5}{6}$xn-1
Γύ$\overline y$=$\frac{1}{n}$Θ®y1+y2+Γ≠+ynΘ©
=$\frac{1}{n}$Θ®$\frac{5}{6}$x1-1+$\frac{5}{6}$x2-1+Γ≠+$\frac{5}{6}$xn-1Θ©
=$\frac{1}{n}$$[{\frac{5}{6}Θ®{x_1}+{x_2}+Γ≠+{x_n}Θ©-n}]$
=$\frac{1}{n}$$[{\frac{5}{6}n\overline x-n}]$=$\frac{5}{6}$$\overline x$-1Θ°
ΒψΤά ±ΨΧβΩΦ≤ι“Μ¥ΈΚ· ΐΒΡ”Π”ΟΘ§ΤΫΨυΒΞΦέΒΡΕ®“εΒ»÷Σ ΕΘ§ΫβΧβΒΡΙΊΦϋ « λΝΖ’ΤΈ’¥ΐΕ®œΒ ΐΖ®»ΖΕ®Κ· ΐΫβΈω ΫΘ§ τ”Ύ÷–ΩΦ≥ΘΩΦΧβ–ΆΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
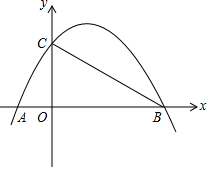 “―÷ΣΒψAΘ®-1Θ§0Θ©Θ§ΒψBΘ®4Θ§0Θ©Θ§ΒψC‘Ύy÷αΒΡ’ΐΑκ÷α…œΘ§«“ΓœACB=90ΓψΘ°≈ΉΈοœΏy=ax2+bx+cΨ≠ΙΐAΓΔBΓΔC»ΐΒψΘ§«“ΕΞΒψΈΣMΘ°
“―÷ΣΒψAΘ®-1Θ§0Θ©Θ§ΒψBΘ®4Θ§0Θ©Θ§ΒψC‘Ύy÷αΒΡ’ΐΑκ÷α…œΘ§«“ΓœACB=90ΓψΘ°≈ΉΈοœΏy=ax2+bx+cΨ≠ΙΐAΓΔBΓΔC»ΐΒψΘ§«“ΕΞΒψΈΣMΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
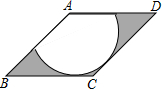 »γΆΦΘ§‘ΎΝβ–ΈABCD÷–Θ§ΓœB=45ΓψΘ§“‘ΒψAΈΣ‘≤–ΡΒΡ…»–Έ”κBCΘ§CDœύ«–Θ§œρ’β―υ“ΜΗωΑ–Ή”…œΥφ“β≈Ή“ΜΟΕΖ…οΎΘ§‘ρΖ…οΎ≤ε‘Ύ“θ”Α«χ”ρΒΡΗ≈¬ ΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§‘ΎΝβ–ΈABCD÷–Θ§ΓœB=45ΓψΘ§“‘ΒψAΈΣ‘≤–ΡΒΡ…»–Έ”κBCΘ§CDœύ«–Θ§œρ’β―υ“ΜΗωΑ–Ή”…œΥφ“β≈Ή“ΜΟΕΖ…οΎΘ§‘ρΖ…οΎ≤ε‘Ύ“θ”Α«χ”ρΒΡΗ≈¬ ΈΣΘ®ΓΓΓΓΘ©| AΘ° | 1-$\frac{3\sqrt{2}Π–}{16}$ | BΘ° | $\sqrt{2}-\frac{3Π–}{8}$ | CΘ° | 1-$\frac{3Π–}{8}$ | DΘ° | $\frac{3Π–}{8}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | a3+a3=a6 | BΘ° | 3a2Γ¬a2=2a2 | CΘ° | Θ®a3Θ©2=a5 | DΘ° | a•a2=a3 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
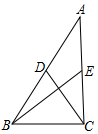 »γΆΦΘ§‘ΎΓςABC÷–Θ§AB=9Θ§AC=7Θ§BEΓΔCDΈΣ÷–œΏΘ§«“BEΓΆCDΘ§‘ρBC=$\sqrt{26}$Θ°
»γΆΦΘ§‘ΎΓςABC÷–Θ§AB=9Θ§AC=7Θ§BEΓΔCDΈΣ÷–œΏΘ§«“BEΓΆCDΘ§‘ρBC=$\sqrt{26}$Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | mΘΨ1 | BΘ° | mΓί1 | CΘ° | mΓί-1«“mΓΌ1 | DΘ° | mΘΨ-1«“mΓΌ1 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
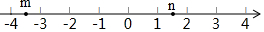 Β ΐmΘ§n‘Ύ ΐ÷α…œΒΡΕ‘”ΠΒψΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
Β ΐmΘ§n‘Ύ ΐ÷α…œΒΡΕ‘”ΠΒψΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©| AΘ° | mΘΨ-3 | BΘ° | mΘΦ-4 | CΘ° | mΘΨn | DΘ° | mΘΦ-n |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com