练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数y ＝ax2＋bx＋ c的图象如图，有以下结论：①a＋b＋c＜0； ②a－b＋c ＞2；③abc＞0；④4a－2b＋c ＜0；⑤c－a＞1．其中所有正确结论的序号是（ ）

    A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤

    【答案】C

    【解析】

    由二次函数的图象可得：a＜0，b＜0，c=2＞0，对称轴x=-1，再结合图象判断各结论即可．

    由图象可得：a＜0，b＜0，c=2＞0，对称轴x=-1，

    ①x=1时，a+b+c＜0，故①正确；

    ②x=-1时，a-b+c＞2，故②正确；

    ③abc＞0，故③正确；

    ④x=-2时，4a-2b+c＞0，故④错误；

    ⑤x=-1时，a-b+c＞2，又=-1，b=2a，c-a＞2>1，故⑤正确，

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

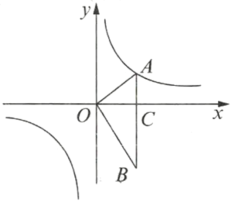
    【题目】如图，在平面直角坐标系中，，轴于点，点在反比例函数的图像上．

    （1）求反比例函数的表达式；

    （2）求面积；

    （3）在坐标轴上是否存在一点，使得以、、三点为顶点的三角形是等腰三角形，若存在，请直接写出所有符合条件的点的坐标；若不存在，简述你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB＝6，AD＝8，沿BD折叠使点A到点A′处，DA′交BC于点F.

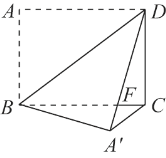
    (1)求证：FB＝FD；

    (2)求证：CA′∥BD；

    (3)求△DBF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形中，，，且，，对角线．

    求证：四边形是矩形；

    如图，若动点从点出发，在边上以每秒的速度向点匀速运动，同时动点从点出发，在边上以每秒的速度向点匀速运动，运动时间为秒，连接、，若，求的值；

    如图，若点在对角线上，，动点从点出发，以每秒的速度沿运动至点止．设点运动了秒，请你探索：从运动开始，经过多少时间，以点、、为顶点的三角形是等腰三角形？请求出所有可能的结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两位同学参加数学综合素质测试，各项成绩如下（单位：分）

    数与代数

    空间与图形

    统计与概率

    综合与实践

    学生甲

    90

    94

    86

    90

    学生乙

    94

    82

    93

    91

    （1）分别计算甲、乙成绩的平均数和方差；

    （2）如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3：3：2：2计算，那么甲、乙的数学综合素质成绩分别为多少分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数yx3的图象与反比例函数y(k为常数，且k0)的图象交于A（1，a），B两点．

    （1）求反比例函数的表达式及点B的坐标；

    （2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

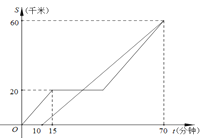
    【题目】甲、乙两车都从A地前往B地，如图分别表示甲、乙两车离A地的距离S（千米）与时间t（分钟）的函数关系.已知甲车出发10分钟后乙车才出发，甲车中途因故停止行驶一段时间后按原速继续驶向B地，最终甲、乙两车同时到达B地，根据图中提供的信息解答下列问题：

    （1）甲、乙两车行驶时的速度分别为多少？

    （2）乙车出发多少分钟后第一次与甲车相遇？

    （3）甲车中途因故障停止行驶的时间为多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，点D、E在BC上，连接AD、AE，如果只添加一个条件使∠DAB=∠EAC，则添加的条件不能为（ ）

    A. BD=CE B. AD=AE C. DA=DE D. BE=CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

    （2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

    查看答案和解析>>

    同步练习册答案