练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．与直线y=x-1平行且经过（2，-3）直线的解析式为y=x-5．

    分析 根据互相平行的两直线解析式的k值相等，设出一次函数的解析式，再把点（2，-3）的坐标代入解析式求解即可．

    解答 解：设所求直线解析式为y=kx+b（k≠0），
    ∵直线y=kx+b与直线y=x-1平行，
    ∴k=1，
    把（2，-3）代入y=x+b得：2+b=-3，
    解得b=-5，
    ∴所求直线解析式为y=x-5．
    故答案是：y=x-5．

    点评 本题考查了待定系数法求函数解析式以及两条直线相交或平行问题，解题时注意：若直线y=k1x+b1与直线y=k2x+b2平行，则k1=k2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．小李有2根木棒，长度分别为10cm和15cm，要组成一个三角形（木棒的首尾分别相连接），第三根木棒的长为（　　）
    A．4cmB．5cmC．20cmD．25cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

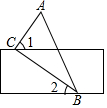    14．如图，将直尺和直角三角板ABC按如图方式摆放，已知∠ACB=90°，∠1=65°，则∠2的大小是（　　）
    A．35°B．30°C．25°D．20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．若函数y=-2mx-（m2-3）的图象经过点（0，1），且y随x的增大而增大．则m=-$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某校开展以“我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制的不完整的折线统计图和扇形统计图．
    （1）在这次随机抽样调查中，共抽查了200名学生；
    （2）把折线统计图补充完整；
    （3）扇形统计图中，公务员部分对应的圆心角的度数72°；
    （4）若从被调查的学生中任意抽取一名，求抽取的这名学生最喜欢的职业是“教师”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．襄阳地区近年来城市发展迅速，交通道路的扩展带动园林绿化的蓬勃发展，襄阳“紫薇公司看到了其中蕴含的商机，经市场调查发现，城市绿化主要需鉴两种不同景观树木．大型造型树木和小型景观乔木．其中大型造型树木和小型景观乔木所投资的金额与市场利涧存在下表所示的函数对应关系．
    大型造型树木小型景观乔木
    投资金额x（万元）x5x24
    市场利润y（万元）y1=kx（k≠0）2y2=ax2+bx（a≠0）2.43.2
    （1）分别求y1和y2的函数解析式；
    （2）有一农户投资10万元加盟“襄阳紫薇公司”对这两种景观树木进行投资，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）如图（1），在Rt△ABC中，∠ACB=90°，∠B=60°，在图中作出∠ACB的三等分线CD，CE．（要求：尺规作图，保留作图痕迹，不写作法）
    （2）由（1）知，我们可以用尺规作图作出直角的三等分线，但是仅仅使用尺规却不能把任意一个角分成三等分，为此，人们发明了许多等分角的机械器具，如图（2）是用三张硬纸片自制的一个最简单的三分角器，与半圆O相接的AB带的长度与半圆的半径相等；BD带的长度任意，它的一边与直线AC形成一个直角，且与半圆相切于点B，假设需要将∠KSM三等分，如图（3），首先将角的顶点S置于BD上，角的一边SK经过点A，另一边SM与半圆相切，连接SO，则SB，SO为∠KSM的三等分线，请你证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

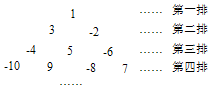    12．将整数1，-2，3，-4，5，-6，…按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示实数9，则表示实数2017的有序实数对是（64，64）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算下列各式：
    （1）-8+12-16-23           
    （2）1$\frac{3}{4}$-2$\frac{1}{6}$-1.75+3$\frac{2}{3}$
    （3）-24×（-$\frac{5}{6}$+$\frac{3}{8}$-$\frac{1}{12}$）        
     （4）-14-$\frac{1}{6}$×[2-（-3）2]×（-2）3．

    查看答案和解析>>

    同步练习册答案