
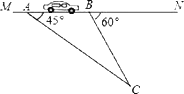
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的 概率是![]() ;中再放进1个黑球,这时取得黑球的概率变为
;中再放进1个黑球,这时取得黑球的概率变为![]()
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y个白球进行摸球游戏。约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 都是实数,且
都是实数,且![]() .我们规定:满足不等式
.我们规定:满足不等式![]() 的实数
的实数![]() 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此一次函数的解析式.
上的“闭函数”,求此一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() , 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .
, 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .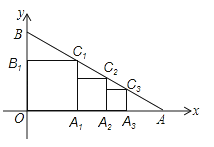
查看答案和解析>>
科目:初中数学 来源: 题型:
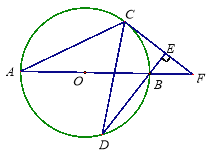
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)当BF=5,![]() 时,求BD的长.
时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=60厘米.
(1)点P沿线段AB自A点向B点以4厘米/分的速度运动,同时点Q沿线段自B点向A点以6厘米/分的速度运动,几分钟后,P、Q两点相遇?
(2)几分钟后,P、Q两点相距20厘米?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为鼓励节约用水,水价实行阶梯计费制,其收费标准如下:
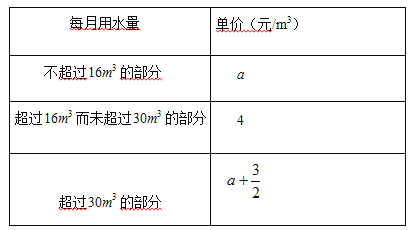
(1)若某用户上月用水22m3,则应缴水费_____元(用含a的代数式表示).
(2)若某用户上月用水36m3,缴水费131元,求a;
(3)在(2)的条件下,设每月用水量xm3,请直接用x的代数式表示每月支出的水费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com