

分析 (1)如图1中,只要证明△AOD是等腰直角三角形即可.
(2)如图2中,连接OE,作OQ⊥CD于Q,作DP⊥AB于P,作OM⊥AD于M.根据$\frac{1}{2}$•AO•DP=$\frac{1}{2}$•AD•OM,求出DP、再证明四边形DPOQ是矩形,在Rt△ODQ中,利用勾股定理即可解决问题.
(3)分两种情形①如图3中,当D在E左侧时,连接OD、OE,作OQ⊥CD于Q,作DP⊥AB于P.则四边形DPOQ是矩形.②如图4中,当D在E右侧时,连接OD、OE,作OQ⊥CD于Q,作DP⊥AB于P.则四边形DPOQ是矩形,分别计算即可.
解答 解:(1)如图1中,连接OD,
∵CD是⊙O切线,
∴OD⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴OD⊥AB,
∴∠AOD=90°,
∵OA=OD=5,
∴∠A=∠ODA=45°,
(2)如图2中,连接OE,作OQ⊥CD于Q,作DP⊥AB于P,作OM⊥AD于M.
∵OA=OD=5,AD=6,OM⊥AD,
∴AM=MD=4,
∴OM=$\sqrt{O{D}^{2}-D{M}^{2}}$=4,
∵$\frac{1}{2}$•AO•DP=$\frac{1}{2}$•AD•OM,
∴DP=$\frac{24}{5}$,
∵AB∥CD,DP∥OQ,
∴四边形DPOQ是平行四边形,∵∠OQD=90°,
∴四边形DPOQ是矩形,
∴OQ=DP=$\frac{24}{5}$,
∵OD=OE,OQ⊥DE,
∴DQ=EQ=$\sqrt{O{D}^{2}-O{Q}^{2}}$=$\sqrt{{5}^{2}-(\frac{24}{5})^{2}}$=$\frac{7}{5}$,
∴CE=CD-DE=10-$\frac{14}{5}$=$\frac{36}{5}$.
(3)如图3中,当D在E左侧时,连接OD、OE,作OQ⊥CD于Q,作DP⊥AB于P.则四边形DPOQ是矩形.
∴OD=OE,OQ⊥DE,
∴QD=QE=3,
∴OQ=$\sqrt{O{D}^{2}-D{Q}^{2}}$=4,
在Rt△APD中,∵DP=OQ=4,AP=OA-OP=OA-DQ=2,
∴AD=$\sqrt{A{P}^{2}+P{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
如图4中,当D在E右侧时,连接OD、OE,作OQ⊥CD于Q,作DP⊥AB于P.则四边形DPOQ是矩形
在Rt△APD中,∵DP=OQ=4,AP=OA+OP=OA+DQ=8,
∴AD=$\sqrt{A{P}^{2}+P{D}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$.
点评 本题考查圆综合题、平行四边形的性质、矩形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线做匀速运动,设运动时间为t(秒),∠APB=y(度),则下列图象中表示y与t之间的函数关系最恰当的是( )
如图,A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线做匀速运动,设运动时间为t(秒),∠APB=y(度),则下列图象中表示y与t之间的函数关系最恰当的是( )| A. | 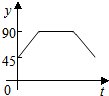 | B. | 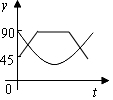 | C. | 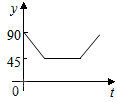 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且CF是⊙O的切线.
如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且CF是⊙O的切线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
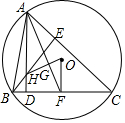 如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )| A. | 2:4 | B. | 1:3 | C. | 2:5 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com