
分析 (1)过C作CH⊥OA,垂足为H,根据线段与角度之间的关系,可求得C点的坐标为(1,$\sqrt{3}$);
(2)①分两种情况讨论,Ⅰ、当0<m≤2时,重合面积为四边形,此时S=S△DEF-S△AGF
Ⅱ、当2<m<4时,重合面积为等边三角形,此时S=S△KAD;
②分0<m≤2和2<m<4两种情况讨论计算,
Ⅰ、如图4,BD+BE转化为BD+BE',而BD+BE'最小,则当D、B、E'三点共线时,BD+BE取得最小值,可求得E$(\frac{7}{3},\sqrt{3})$.
Ⅱ、同Ⅰ的方法即可得出m=4,不符合要求.
解答 解:(Ⅰ)如图1,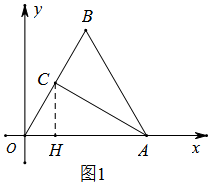
过C作CH⊥OA,垂足为H,
∵OA=4,△OAB为等边三角形,
∴∠BOA=60°,OB=4,
∵C为OB的中点,
∴OC=2,∠OCA=90°,
∴∠OCH=30°,
∴OH=$\frac{1}{2}OC$=1,CH=$\sqrt{O{C}^{2}-O{H}^{2}}=\sqrt{3}$,
∴点C的坐标为(1,$\sqrt{3}$);
(Ⅱ)①∵△DEF是△OCA平移得到的,
∴AF=OD=m,
当0<m≤2时,如图2,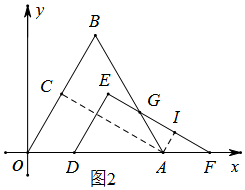
设AB与EF交于点G,
过点A作AI⊥EF,垂足为I,
∵∠BAF=120°,∠DFE=30°,
∴∠AGF=30°,
∴AI=$\frac{1}{2}$m,GF=2FI=$\sqrt{3}m$,
∴S=S△DEF-S△AGF=2$\sqrt{3}$-$\frac{\sqrt{3}}{4}$m2,
当2<m<4时,如图3,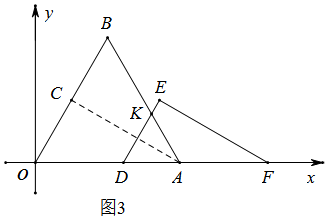
设AB与DE交于点K
∵∠KDA=∠KAD=60°,
∴△KAD为等边三角形,
∵DA=4-m,
∴S=S△KAD=$\frac{\sqrt{3}}{4}$(4-m)2,
综上所述:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{4}(8-{m}^{2}),0<m≤2}\\{\frac{\sqrt{3}}{4}(4-{m}^{2}),2<m<4}\end{array}\right.$;
②Ⅰ、当0<m≤2时,如图4, 过点B作直线l∥x轴,
过点B作直线l∥x轴,
作点E关于直线l的对称点E',直线l的解析式为y=2$\sqrt{3}$,
连接BE,BE',
∴BE=BE',
∴BD+BE=BD+BE',要使BD+BE最小,
∴BD+BE'最小,
即:点D,B,E'三点共线,
∵△OAC沿x轴向右平移得到△DFE,设OD=m,
∴CE=OD=m,D(m,0),
由(1)知,C(1,$\sqrt{3}$),
∴E(m+1,$\sqrt{3}$),
∵点E关于直线l的对称点E',
∴E'(m+1,3$\sqrt{3}$),
由点D(m,0),E'(m+1,3$\sqrt{3}$),得出直线DE'的解析式为y=3$\sqrt{3}$x-3$\sqrt{3}$m,
∵点B在直线DE'上,
∴3$\sqrt{3}$×2-3$\sqrt{3}$m=2$\sqrt{3}$,
∴m=$\frac{4}{3}$,
∴E$(\frac{7}{3},\sqrt{3})$.
Ⅱ、当2<m<4时,作点E关于直线l的对称点E',连接BE,BE',
∴BE=BE',
∴BD+BE=BD+BE',要使BD+BE最小,
∴BD+BE'最小,
即:点D,B,E'三点共线,
∵△OAC沿x轴向右平移得到△DFE,设OD=m,
∴CE=OD=m,D(m,0),
由(1)知,C(1,$\sqrt{3}$),
∴E(m+1,$\sqrt{3}$),
∵点E关于直线l的对称点E',
∴E'(m+1,$\sqrt{3}$),
由点D(m,0),E'(m+1,$\sqrt{3}$),得出直线DE'的解析式为y=$\sqrt{3}$x-$\sqrt{3}$m,
∵点B在直线DE'上,
∴$\sqrt{3}$×2-$\sqrt{3}$m=2$\sqrt{3}$,
∴m=0(舍去)
∴当BD+BE取最小值时,点E的坐标为$(\frac{7}{3},\sqrt{3})$.
点评 此题是几何变换综合题,以三角形为背景,考查等边三角形的性质、平移的性质、待定系数法,用面积割补法来求不规则图形的面积,对称的性质,体现了分类讨论的思想,确定出直线DE'的解析式是解本题的关键,借助点D,E'的横坐标相差1,此题(2)②容易丢点第二种不成立的理由.


科目:初中数学 来源: 题型:选择题
| A. | x≠1 | B. | x≥-$\frac{1}{2}$ | C. | x≥-$\frac{1}{2}$且x≠1 | D. | x>-$\frac{1}{2}$且x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
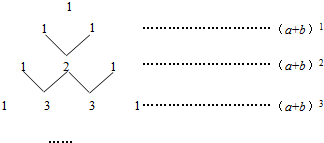
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
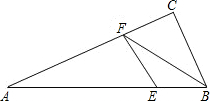 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )| A. | $\frac{5\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com