

���� ��1���������к����Ķ��弰��A��������⣻
��2����Ϊ��C��A��B���������ϣ��ʴ����������з�������⼴�ɣ�
��3���õ�EB=-��1+m����FB=-m����Ӽ�����⣻
��4������CD����ΪBCΪԲ��ֱ�������ԡ�BDC=90�㣬��BD=$\frac{1}{2}$AB����֤��CA=CB���ɴ˿���÷�������ĵ�C��-$\frac{3}{2}$��0����
��� �⣺��1����tan��ABO=$\frac{OA}{OB}=\frac{1}{2}$����A��1��0����
��OB=2��������B��������0��2����
��2����C��m��0����A��1��0����B��0��2����������y=ax2+bx+c�ϣ�
��$\left\{\begin{array}{l}{a+b+c=0}\\{c=2}\\{a{m}^{2}+bm+c=0}\end{array}\right.$
��֮�ã�b=-$\frac{2��m+1��}{m}$��a=$\frac{2}{m}$��
��x=-$\frac{b}{2a}$=$\frac{m+1}{2}$��
���������ߵĶԳ���Ϊx=$\frac{m+1}{2}$
��3����EB=-��1+m����FB=-m��EF=FB-EB=1��
���߶�EF�ij��Ƕ�ֵ��
��4������ͼ��ʾ������CD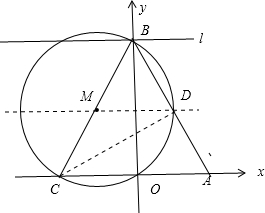
��BCS�ǡ�M��ֱ����
���CDB=90�㣬
����BD=$\frac{1}{2}$AB����BD=DA
����֤CB=CA
��$\sqrt{{2}^{2}+{m}^{2}}$=1-m
��֮��m=-$\frac{3}{2}$��
��������һ��C��-$\frac{3}{2}$��0����ʹ��BD=$\frac{1}{2}$AB
���� ���⿼���˶��κ�����Բ���й�֪ʶ�㣬����Ĺؼ��Ǻ���ͼ���ϵĵ��������ʽ�Ĺ�ϵ�Լ�Բ�Ļ���֪ʶ����ۺϷ��������������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��A1B1C1�Ķ�������ֱ���A1��1��5����B1��0��2����C1��6��1��������A1B1C1������һ��M1��x0��y0������ƽ�ƺ��Ӧ��ΪM��x0-2��y0-1��������A1B1C1��ͬ����ƽ�ƣ��õ���ABC��
��A1B1C1�Ķ�������ֱ���A1��1��5����B1��0��2����C1��6��1��������A1B1C1������һ��M1��x0��y0������ƽ�ƺ��Ӧ��ΪM��x0-2��y0-1��������A1B1C1��ͬ����ƽ�ƣ��õ���ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪�߶�DE�����߶�ABƽ�Ƶõ��ģ���AB=DC=4cm��EC=3cm�����DCE���ܳ�Ϊ11���ף�
��֪�߶�DE�����߶�ABƽ�Ƶõ��ģ���AB=DC=4cm��EC=3cm�����DCE���ܳ�Ϊ11���ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ѡ�ABC�Ƶ�C˳ʱ����ת35��õ���A��B��C��A��B�佻AC�ڵ�D������A��=55�㣬��B=50�㣬���ACB��Ķ����ǣ�������
��ͼ���ѡ�ABC�Ƶ�C˳ʱ����ת35��õ���A��B��C��A��B�佻AC�ڵ�D������A��=55�㣬��B=50�㣬���ACB��Ķ����ǣ�������| A�� | 35�� | B�� | 40�� | C�� | 45�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�PQ��BC����S��APQ=3��S��PQB=6����S��CQB=��������
��ͼ���ڡ�ABC�У�PQ��BC����S��APQ=3��S��PQB=6����S��CQB=��������| A�� | 10 | B�� | 16 | C�� | 6 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��P��1��-3�����ʶ����� | B�� | ��֪��A��-3��4������B��-3��2������AB��x�� | ||
| C�� | ��M��3��-2����y��ľ���Ϊ2����λ | D�� | ��֪��A��1��2������B��-2��-1������AB=3$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
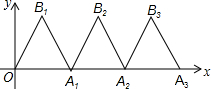 ��ͼ��������OB1A1����f1������A1��4��0����OB1=A1B1����OB1A1=60�㣬���ν�f1��x��������ƽ��4����λ��f2���ٽ�f2����ƽ��4����λ��f3��������P��23��n����f6�ϣ���n��ֵ�ǣ�������
��ͼ��������OB1A1����f1������A1��4��0����OB1=A1B1����OB1A1=60�㣬���ν�f1��x��������ƽ��4����λ��f2���ٽ�f2����ƽ��4����λ��f3��������P��23��n����f6�ϣ���n��ֵ�ǣ�������| A�� | 0 | B�� | $\sqrt{3}$ | C�� | 2$\sqrt{3}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com