
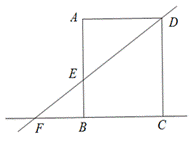
��ͼ���ھ���ABCD�У�AD=8��ֱ��DE��ֱ��AB�ڵ�E����ֱ��BC��F��AE=6.
��1������P�DZ�AD�ϵ�һ�����㣨�����A��D�غϣ���PH��DE��H����DPΪx,�ı���AEHP�����Ϊy,����y��x�ĺ�������ʽ��
��2����AE=2EB.
����Բ����ֱ��BC�ϣ�����ֱ��DE��AB�����еġ�O�İ뾶����
�ڰ뾶Ϊ4��Բ����ֱ��DF�ϣ��������ABCD������һ������ֱ�����е�Բ���ж��ٸ�����ֱ��д������������Բ�ĸ�������.��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
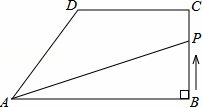
��ͼ����ֱ������ABCD�У�AB��DC����ABC=90�㣬AB=8cm��BC=4cm��CD=5cm������P�ӵ�B��ʼ������BC��CD��DA��1cm/s���ٶ��˶�����A�����P�˶���ʱ��Ϊt��s������PAB���ΪS��cm2����
��1����t=2ʱ����S��ֵ��
��2������P�ڱ�DA���˶�ʱ����S����t�ĺ�������ʽ��
��3����S=12ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��1��д��һ��ֻ����ĸx������ʽ��Ҫ��˴���ʽ�����壬��ĸx����ȡȫ�����1��ʵ�����Ҵ˴���ʽ��ֵ��Ϊ������
��2����x�Ƿ���x2-x-2=0�ĸ�����1���д���ʽ��ֵ.
�������ͼ�������ҿ����⣬�����ʽ�����壬���θ�ʽ�ı�������Ϊ�Ǹ��������̵Ľ⣬����ѧ��˼ά��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һũ�����г����У���ʱ�г��ϵĴм���1.00Ԫһ�һ�з���ũ��˵�����������Ĵзֿ�����Ҷ0.50Ԫһ��а�0.50Ԫһ���ũ�����˴з��Ļ�������˼���ͰѴ�ȫ�����꣮��ũ������Ǯ֮��ŷ���ֻ����һ��Ǯ����ʱ�з��Ѳ�����Ӱ���������㣬��������ѧ���ԽҴ��з��İ�Ϸ��
�������£�������z���Ҷx��а�y��з���
��x+y=z���������з���ǮΪ0.5x+0.5y=0.5z��
��ʵ��Ӧ����ǮΪ1.0x+1.0y=1.0z�����һĿ��Ȼ���Ǵз�ֻ����һ��Ǯ���������дУ�
���ʶ�������ǣ������ڳԴе�ʱ����Ҫ�Ե��Ǵаף��а�Ӧ�ȴ�Ҷ���Ĺ�
����һ���еĴ�Ҷ�ʹа�������ͬ����Ҷ�ʹаļ�Ǯ֮������1.00Ԫ��������ѧ����˵����ʱũ������ֻ����һ���Ǯ��
����һ���еĴ�Ҷ�ʹа�������ͬ���Ҵ�Ҷ���������ڴа���������Ҷ0.20Ԫһ��а�0.80Ԫһ�������ѧ����˵����ʱũ������Ǯ����һ�룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
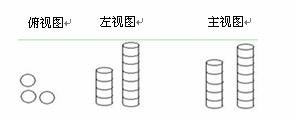
�����ϰڷ�ͬһ�ֺ�װ�ɿ�����������ͼ��ͼ��ʾ��������Ϲ��ڷ��ɿ���Ϊ�� ��
A��15�� B��16�� C��18�� D��20��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ABC�У�E��F�ֱ���AB,AC���е㣬����AEF�����Ϊ1�����ı���EBCF�����Ϊ ( )
A��2 B��3 C��4 D��5

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ҹ������ݰ˺ŷɴ���˳�����գ�����ɴ�����ǰ10���Ϊ��10�룬��ô�ɴ������15��
���� ��
A����10�� B����10�� C����15�� D����15��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com