
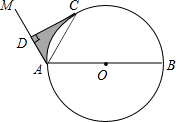
 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.
如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.分析 (1)先证明OC∥AM,由CD⊥AM,推出OC⊥CD即可解决问题.
(2)根据S阴=S△ACD-(S扇形OAC-S△AOC)计算即可.
解答 (1)证明: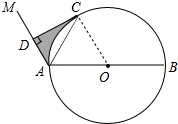 连接OC.
连接OC.
∵OA=OC.
∴∠OAC=∠OCA,
∵∠MAC=∠OAC,
∴∠MAC=∠OCA,
∴OC∥AM,
∵CD⊥AM,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)解:在RT△ACD中,∵∠ACD=30°,AD=4,∠ADC=90°,
∴AC=2AD=8,CD=$\sqrt{3}$AD=4$\sqrt{3}$,
∵∠MAC=∠OAC=60°,OA=OC,
∴△AOC是等边三角形,
∴S阴=S△ACD-(S扇形OAC-S△AOC)
=$\frac{1}{2}$×4×4$\sqrt{3}$-($\frac{60•π•{8}^{2}}{360}$-$\frac{\sqrt{3}}{4}$×82)
=24$\sqrt{3}$-$\frac{32}{3}$π.
补充等边三角形面积公式:设等边三角形△AOC的边长为a,作CD⊥AO于D.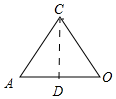
在Rt△ACD中,∵∠ADC=90°,AC=a,∠A=60°,
∴∠ACD=30°,
∴AD=$\frac{1}{2}$a,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{a}^{2}-(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{3}}{2}$a,
∴S△AOC=$\frac{1}{2}$•OA•CD=$\frac{1}{2}$•a•$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{4}$a2.
点评 本题考查切线的判定、扇形的面积,解题的关键是熟练掌握切线的判定方法,学会利用分割法求面积,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
| 尺码/cm | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 销售量/双 | 5 | 6 | 8 | 12 | 5 | 3 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2+11 | B. | (x+3)2-7 | C. | (x-3)2-7 | D. | (x+3)2+11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查乘坐飞机的旅客是否携带违禁物品 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查市场上老酸奶的质量情况 | |
| D. | 调查我市市民对伦敦奥运会吉祥物的知晓率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com