

分析 (1)利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠GEH=90°,进而求出四边形EGFH是矩形;
(2)利用菱形的判定方法要证?MNQP是菱形,只要证MN=NQ即可.
解答 (1)证明:∵EH平分∠BEF,
∴∠FEH=$\frac{1}{2}$∠BEF,
∵FH平分∠DFE,
∴∠EFH=$\frac{1}{2}$∠DFE,
∵AB∥CD,
∴∠BEF+∠DFE=180°,
∴∠FEH+∠EFH=$\frac{1}{2}$(∠BEF+∠DFE)=$\frac{1}{2}$×180°=90°,
∵∠FEH+∠EFH+∠EHF=180°,
∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°,
同理可得:∠EGF=90°,
∵EG平分∠AEF,
∴∠GEF=$\frac{1}{2}$∠AEF,
∵EH平分∠BEF,
∴∠FEH=$\frac{1}{2}$∠BEF,
∵点A、E、B在同一条直线上,
∴∠AEB=180°,
即∠AEF+∠BEF=180°,
∴∠FEG+∠FEH=$\frac{1}{2}$(∠AEF+∠BEF)=$\frac{1}{2}$×180°=90°,
即∠GEH=90°,
∴四边形EGFH是矩形;
(2)解:由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,
要证?MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,
故只要证GM=FQ,即证△MGE≌△QFH,易证 GE=FH、∠GME=∠FQH.
故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH;再证出NG=NF,即可得证.
理由如下:∵MN∥EF,PQ∥EF,
∴∠MGE=∠GEF,MN∥PQ,
∵AB∥CD,
∴四边形MNQP是平行四边形,
∴∠GME=∠FQH,
由(1)得:∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,GE=FH,
∴∠MGE=∠QFH,
在△MGE和△QFH中,$\left\{\begin{array}{l}{∠GME=∠FQH}&{\;}\\{∠MGE=∠QFH}&{\;}\\{GE=FH}&{\;}\end{array}\right.$,
∴△MGE≌△QFH(AAS),
∴GM=FQ,
∵∠MGE=∠QFH,∠EGF=∠HFG=90°,
∴∠NGF=∠NFG,
∴NG=NF,
∴MN=NQ,
∴四边形MNQP是菱形.
点评 此题主要考查了矩形的判定以及菱形的判定和角平分线的性质,根据题意得出证明菱形的方法是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )| A. | PC=PD | B. | ∠CPO=∠DOP | C. | ∠CPO=∠DPO | D. | OC=OD |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省揭阳市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
函数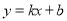 (
(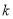 、
、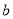 为常数,
为常数,  )图象如图所示,则关于
)图象如图所示,则关于 的不等式
的不等式 的解集为( )
的解集为( )

A.  B.
B. 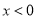 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥2 | B. | 2≤x≤4 | C. | x<4 | D. | 2<x<4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
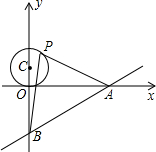 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )| A. | 10 | B. | 9 | C. | 6+$\frac{5\sqrt{2}}{2}$ | D. | 9$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com