
【题目】如图,![]() 平分
平分![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,
,![]() .求四边形
.求四边形![]() 的面积.
的面积.
【答案】(1)∠CDA=120°;(2)9
【解析】
(1)根据角平分线的性质得到AE=AF,进而证明Rt△ABE≌Rt△ADF(HL),再根据全等三角形的性质即可得到∠CDA的度数;
(2)先证明Rt△ACE与Rt△ACF(HL),得到CE=CF,再得到CE的长度,将四边形![]() 的面积分成△ACE与△ACD的面积计算即可.
的面积分成△ACE与△ACD的面积计算即可.
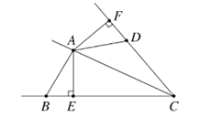
解:(1)∵![]() 平分
平分![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]()
∴AE=AF,∠AEB=∠AFD=90°,
在Rt△ABE与Rt△ADF中
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL)
∴∠ABE=∠ADF=60°,
∴∠CDA=180°-∠ADF=120°,
故∠CDA=120°.
(2)由(1)可得Rt△ABE≌Rt△ADF
∴BE=DF,
又∵在Rt△ACE与Rt△ACF中
![]()
∴Rt△ACE与Rt△ACF(HL)
∴CE=CF
CE=CF=CD+DF=CD+BE=5,
又∵![]()
∴AF=AE=2
∴四边形AECD的面积=![]()
故四边形![]() 的面积为9
的面积为9


科目:初中数学 来源: 题型:
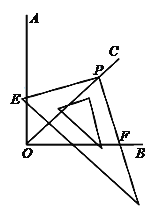
【题目】如图,∠AOB=90°,将三角尺的直角顶点P落在∠AOB的平分线OC的任意一点上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。证明:PE=PF。
查看答案和解析>>
科目:初中数学 来源: 题型:
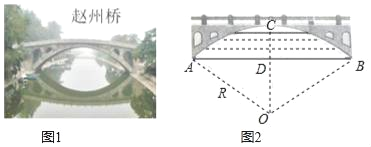
【题目】赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,
(1)如图1,尺规作图,找到桥弧所在圆的圆心O(保留作图痕迹);
(2)如图2,求桥弧AB所在圆的半径R.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
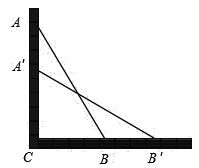
【题目】如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
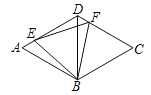
【题目】如图所示,△ABD和△BCD都是等边三角形,E、F分别是边AD、CD上的点,且DE=CF,连接BE、EF、FB.
求证:(1)△ABE≌△DBF;
(2)△BEF是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡顶![]() 处的同一水平面上有一座古塔
处的同一水平面上有一座古塔![]() ,数学兴趣小组的同学在斜坡底
,数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求古塔
.求古塔![]() 的高度.(结果精确到
的高度.(结果精确到![]() 米,参考数据:
米,参考数据: ![]() ,
, ![]() ,
, ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在右边的平面直角坐标系中描出以下三点:![]() 、
、![]() 、
、![]() 并回答如下问题:
并回答如下问题:
![]() 在平面直角坐标系中画出△ABC;
在平面直角坐标系中画出△ABC;
![]() 在平面直角坐标系中画出△A′B′C′;使它与
在平面直角坐标系中画出△A′B′C′;使它与![]() 关于x轴对称,并写出点C′的坐标______;
关于x轴对称,并写出点C′的坐标______;
![]() 判断△ABC的形状,并说明理由.
判断△ABC的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com